
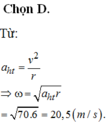
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

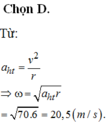

Ta có: \(\omega=\dfrac{\pi}{6}\) rad/s
Gia tốc hướng tâm:
\(a_{ht}=r\cdot\omega^2=2\cdot\dfrac{\pi}{6}=\dfrac{\pi}{3}\)m/s2

Một quạt máy quay với tốc độ góc 30 rad/s. Cánh quạt dài 80cm. Tính gia tốc hướng tâm của một điểm ở đầu cánh quạt
. A. 72000m/s2
B. 720 m/s2
C. 1125m/s2
D. 24 m/s2
Bài giải:
Gia tốc hướng tâm:
\(a_{ht}=r\cdot\omega^2=0,8\cdot30^2=720\)m/s2
Chọn B.

Bánh xe quay đều với tốc độ góc ω = 2π (rad/s).
Do đó một điểm M thuộc vành ngoài bánh xe cũng quay đều với cùng tốc độ góc ω = 2π (rad/s).
Chu kỳ quay của M: T = 2π/ω = 1 (s).
Tần số quay của M: f = 1/T = 1 Hz.
Tốc độ dài của M: v = R.ω = 0,3.2π = 0,6π (m/s) ≈ 1,9 (m/s).
Gia tốc hướng tâm của M: an = R.ω2 = 0,3.(2π)2 = 12 m/s2.

a)
Lấy g = 10m/s2
Gia tốc hướng tâm của nhà du hành là:
aht = 7g = 70 (m/s2)
Tốc độ dài của nhà du hành là:
v2 = aht. r = 70.5 = 350
=> v ≈ 18,7 (m/s)
b)
Tốc độ góc của người đó là:
ω2 = aht/r = 70/5 = 14
=> ω ≈ 3,74 (rad/s)
Tần số chuyển động là:
f = ω/(2.3,14) ≈ 0,6 (vòng/s) = 36 vòng/phút