
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

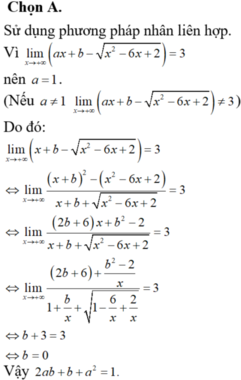

1.
\(\lim\dfrac{5\sqrt{3n^2+n}}{2\left(3n+2\right)}=\lim\dfrac{5\sqrt{3+\dfrac{1}{n}}}{2\left(3+\dfrac{2}{n}\right)}=\dfrac{5\sqrt{3}}{6}\Rightarrow a+b=11\)
2.
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax+b}{x-2}=6\) khi \(x^2+ax+b=0\) có nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(x+a+2\right)=a+4\Rightarrow a+4=6\Rightarrow a=2\Rightarrow b=-8\)
\(\Rightarrow a+b=-6\)

Giới hạn đã cho hữu hạn nên \(a=-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(b-x\right)^2-\left(x^2-6x+2\right)}{b-x+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(6-2b\right)x+b^2-2}{-x+\sqrt{x^2-6x+2}+b}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{6-2b+\dfrac{b^2-2}{x}}{-1-\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}+\dfrac{b}{x}}=\dfrac{6-2b}{-2}=5\)
\(\Rightarrow b=8\)
Cả 4 đáp án đều sai, số lớn hơn là 8

\(\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{\dfrac{x^2}{x^2}-\dfrac{3x}{x^2}}+\dfrac{ax}{x}}{\dfrac{bx}{x}-\dfrac{1}{x}}=\dfrac{a-1}{b}=3\)
=> A

\(a+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=0\) có nghiệm \(x=1\)
\(\Rightarrow a+\dfrac{2}{\sqrt{1}}-\dfrac{6}{\sqrt{1}}=0\Rightarrow a=4\)
\(4+\dfrac{x+1}{\sqrt{x^2-x+1}}-\dfrac{3x+3}{\sqrt{x}}=3\left(2-\dfrac{x+1}{\sqrt{x}}\right)+\left(\dfrac{x+1}{\sqrt{x^2-x+1}}-2\right)\)
\(=-3\left(\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(x+1+2\sqrt{x}\right)}\right)+\dfrac{-3\left(x-1\right)^2}{\sqrt{x^2-x+1}\left(x+1-2\sqrt{x^2-x+1}\right)}\)
Rút gọn với \(\left(x-1\right)^2\) bên ngoài rồi thay dố là được

Để giới hạn đã cho là hữu hạn thì \(a=1\)
\(\lim\limits_{x\rightarrow+\infty}\left(x+b-\sqrt{x^2-6x+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+2bx+b^2-\left(x^2-6x+2\right)}{x+b+\sqrt{x^2-6x+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2b+6\right)x+b^2-2}{x+b+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{2b+6+\dfrac{b^2-2}{x}}{1+\dfrac{b}{x}+\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}}=\dfrac{2b+6}{2}=b+3\)
\(\Rightarrow b+3=3\Rightarrow b=0\Rightarrow\left\{{}\begin{matrix}a=1\\b=0\end{matrix}\right.\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{3x^2+2}-\sqrt{4+x}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{3x^2-x-2}{\sqrt{3x^2+2}+\sqrt{4+x}}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{3x+2}{\left(x+1\right)\left(\sqrt{3x^2+2}+\sqrt{4+x}\right)}=\dfrac{5}{2.2\sqrt{5}}=\dfrac{\sqrt{5}}{4}\).
Từ đó a = 5; b = 4 nên a - b = 1.

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

Bài 1:
a. \(\lim\limits_{x\rightarrow-1}\frac{x^5+1}{x^3+1}=\lim\limits_{x\rightarrow-1}\frac{5x^4}{3x^2}=\frac{5}{3}\)
b. \(\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+x}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4+1}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{120x^4-100x^3}{2}=\frac{120-100}{2}=10\)
c. \(\lim\limits_{x\rightarrow0}\frac{\left(1+2x\right)\left(1+3x\right)x}{x}+\lim\limits_{x\rightarrow0}\frac{\left(1+3x\right)2x}{x}+\lim\limits_{x\rightarrow0}\frac{3x+1-1}{x}=1+2+3=6\)
d. \(\lim\limits_{x\rightarrow0}\frac{\left(1+x\right)^5-\left(1+5x\right)}{x^5+x^2}=\lim\limits_{x\rightarrow0}\frac{5\left(1+x\right)^4-5}{5x^4+2x}\)
\(=\lim\limits_{x\rightarrow0}\frac{20\left(1+x\right)^3}{20x^3+2}=\frac{20}{2}=10\)
Bài 2:
\(\lim\limits_{x\rightarrow1}\frac{x^m-1}{x^n-1}=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)
\(\lim\limits_{x\rightarrow a}\frac{x-a}{x^n-a^n}=\lim\limits_{x\rightarrow a}\frac{1}{nx^{n-1}}=\frac{1}{n.a^{n-1}}\)

Trình bày công thức các thứ khá dài nên tôi thử nói hướng, nếu bạn hiểu đc và làm đc thì ok còn nếu k hiểu thì bảo mình, mình làm full cho
Bây giờ phân tích mẫu trước, ra (x-1)2(x+2)
Để cái lim này nó ra đc 1 số thực thì tử và mẫu cùng phải triệt tiêu (x-1)2 đi, tức là tử phải chia hết (x-1)2, tức là tử cũng phải có nghiệm kép x=1
Do đó \(\left\{{}\begin{matrix}f\left(1\right)=0\\f'\left(1\right)=0\end{matrix}\right.\)

a. \(lim_{x\rightarrow3}\dfrac{x^3-27}{3x^2-5x-2}=\dfrac{3^3-27}{3.3^2-5.3-2}=\dfrac{0}{10}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{x+2}-2}{4x^2-3x-2}=\dfrac{\sqrt{2+2}-2}{4.2^2-3.2-2}=\dfrac{0}{8}=0\)
c. \(lim_{x\rightarrow1}\dfrac{1-x^2}{x^2-5x+4}=lim_{x\rightarrow1}\dfrac{\left(1-x\right)\left(x+1\right)}{\left(x-1\right)\left(x-4\right)}=lim_{x\rightarrow1}\dfrac{-\left(x+1\right)}{x-4}=\dfrac{-\left(1+1\right)}{1-4}=\dfrac{2}{3}\)
d. Câu này mình chịu, nhìn đề hơi lạ so với bình thường hehe