Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Bổ đề : ![]()
Trong đó : + U L max là giá trị cực đại của U L khi L thay đổi.
+ φ 0 là độ lệch pha của u và i trong trường hợp U L max.
Áp dụng :
U
L
như nhau thì ![]()
Có 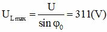
![]()

Giải thích: Đáp án B
Khi C = C1, độ lệch pha của mạch: 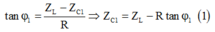
Khi C = C2, độ lệch pha của mạch: 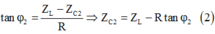
Từ (1) và (2) ta có: ![]()
Lấy (1). (2) ta có: ![]()
Khi C = C0, độ lệch pha của mạch:
Mà khi C = C1 và C = C2 điện áp hiệu dụng ở hai đầu tụ điện có cùng giá trị:
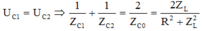
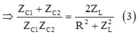
Từ (1), (2) và (3):
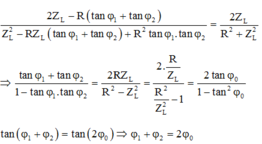

Mình giải thích rõ hơn công thức của bạn Nguyễn Trung Thành
Nhận xét:
+ Khi L thay đổi thì góc b và c không đổi (do R và ZC không đổi).
+ Khi L = L0 để UL max thì a0 + b = 900.
Áp dụng định lí hàm số sin trong tam giác OULUC:
\( \frac{U_L}{\sin(a+b)}=\frac{U}{\sin c}=const\)
\(\Rightarrow\frac{U_L}{\sin(a_1+b)}=\frac{U_L}{\sin(a_2+b)}\Rightarrow \sin(a_1+b)=\sin(a_2+b)\Rightarrow a_1+b=\pi-(a_2+b)\)
\(\Rightarrow a_1+a_2=\pi-2b\) Mà \(a_0+b=\frac{\pi}{2}\Rightarrow 2a_0=\pi-2b\)
\(\Rightarrow a_1+a_2=2a_0\)
Hay: \(\varphi_0=\frac{\varphi_1+\varphi_2}{2}\)
Áp dụng công thức: \(\varphi_0=\frac{\varphi_1+\varphi_2 }{2}\Rightarrow\varphi_0=\frac{0,56+0,98 }{2}=0,77\)
\(\Rightarrow \cos\varphi_0=\cos0,77=0,72\)
Đáp án B.

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
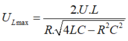
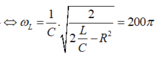
Và điện áp trên tụ cực đại là:
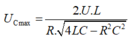
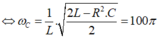
Dễ thấy:
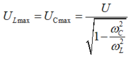
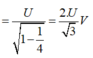

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
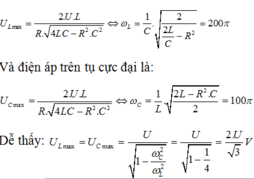
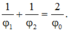
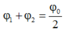
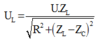
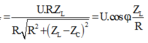
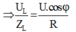
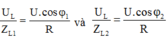
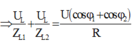
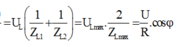
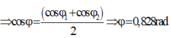

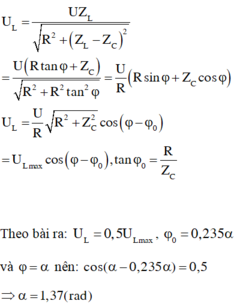
Ta biễu diễn trên giãn đồ vecto. Hai giá trị của L cho cùng một điện áp hiệu dụng trên cuộn cảm → U 1 → và U 2 → đối xứng với ứng với U L m a x
→ Ta có φ 1 + φ 2 = 2 φ 0 → φ 0 = 0 , 785 rad.
Đáp án C