Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
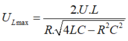
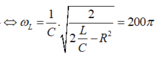
Và điện áp trên tụ cực đại là:
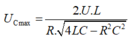
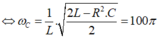
Dễ thấy:
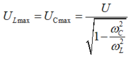
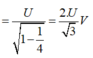

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
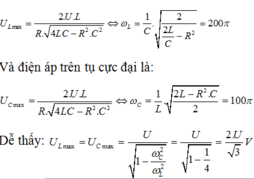

Đáp án A
+ Khi U c m a x ⇒ ω = ω c = 1 L C - R 2 2 L 2 = 100 π
+ Khi U L m a x ⇒ ω = ω L = 2 2 L C - R 2 C 2 = 200 π
+ ω L = 2 ω C ⇒ R 2 = L C ⇒ R = L C
+ U L m a x = 2 U L R 4 L C - R 2 C 2 = 2 U L L C 4 L C - L C C 2 = 2 U 3

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Đáp án A
Phương pháp: sử dụng điều kiện cực đai của UL khi tần số góc biến đổi
Cách giải: Tần số góc biến thiên để ULmax nên ta có:
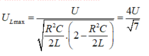
Đặt R 2 C 2 L = x ⇒ x = 1 4 Khi tần số góc là ω 1 thì:

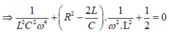
Áp dụng định lý vi et phương trình có hai nghiệm phân biệt thỏa mãn:
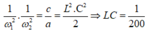
Từ 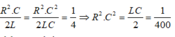
Mặt khác ta lại có:

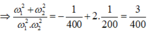
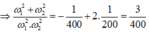
Biết tổng và tích ta tìm ra được

Vậy ω 1 = 10 2

Đáp án A
Điện áp hiệu dụng trên tụ điện:
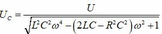
→ Hai nghiệm ω 1 2 và ω 2 2 cho cùng một giá trị U C thỏa mãn ω 1 2 + ω 2 2 = 2 ω C 2

Đáp án B
I = U R 2 + ω L - 1 ω L 2 . Theo bài I 1 = I 2 = I m a x 5 hay Z 1 = Z 2 = 5 Z
R 2 + L ω 1 - 1 C ω 1 2 = R 2 + L ω 2 - 1 C ω 2 2 = 5 R
Kết hợp với ω1 > ω2 → khi ω = ω1 mạch có tính cảm kháng, khi ω = ω2 mạch có tính dung kháng.
L ω 1 - 1 C ω 1 = 2 R L ω 2 - 1 C ω 2 = - 2 R ⇒ L ω 1 2 - ω 2 2 = 2 R ω 1 + ω 2 ⇒ R = L ω 1 - ω 2 2 = 25 Ω
Đáp án B