Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//DC

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

A B E D F C H K
a) \(\Delta DMC=\Delta AMB\left(c.g.c\right)\)
b) Ta có: \(AB+BE=CD+CF\)
mà \(AB=CD\left(a\right);BE=CF\left(gt\right)\)
\(\Rightarrow AE=DF\) (1)
Có: \(\widehat{EAM}=\widehat{FDM}\) (suy từ câu a) (2)
và AM = DM (gt) (3)
Từ (1); (2) và (3) \(\Rightarrow\Delta EAM=\Delta FDM\left(c.g.c\right)\)
\(\Rightarrow EM=MF\)
từ đó cũng c/m được: \(E,M,F\) thẳng hàng
\(\Rightarrow M\) là trung điểm của EF.
c) Xét \(\Delta AKM;\Delta DHM\) vuông tại K; H:
\(AM=DM\)
\(\widehat{AMK}=\widehat{DMH}\) (đ2)
\(\Rightarrow\Delta AKM=\Delta DHM\left(ch-gn\right)\)
\(\Rightarrow AK=DH.\)
a) \(\Delta DMC=\Delta AMB\left(c.g.c\right)\)
=> góc DCM = góc ABM (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong nên DC // AB (đpcm)
b) cần chứng minh thêm E, M, F thẳng hàng
c) gần TT câu a

a. Hình vẽ (0.5 điểm)
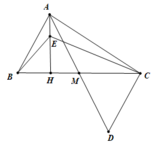
Xét ΔABM và ΔDCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔDCM (c.g.c) (0.5 điểm)
⇒ AB = DC (hai cạnh tương ứng) (0.5 điểm)

Bài 2
Bài làm
a) Xét tam giác ABM và tam giác DCM có:
BM = MC ( Do M là trung điểm BC )
^AMB = ^DMC ( hai góc đối )
MD = MA ( gt )
=> Tam giác ABM = tam giác DCM ( c.g.c )
b) Xét tam giác BHA và tam giác BHE có:
HE = HA ( Do H là trung điểm AE )
^BHA = ^BHE ( = 90o )
BH chung
=> Tam giác BHA = tam giác BHE ( c.g.c )
=> AB = BE
Mà tam giác ABM = tam giác DCM ( cmt )
=> AB = CD
=> BE = CD ( đpcm )
Bài 3
Bài làm
a) Xét tam giác ABD và tam giác ACD có:
AB = AB ( gt )
BD = DC ( Do M là trung điểm BC )
AD chung
=> Tam giác ABD = tam giác ACD ( c.c.c )
b) Xét tam giác BEC và tam giác MEA có:
AE = EC ( Do E kà trung điểm AC )
^BEC = ^MEA ( hai góc đối )
BE = EM ( gt )
=> Tam giác BEC = tam giác MEA ( c.g.c )
=> BC = AM
Mà BD = 1/2 . BC ( Do D là trung điểm BC )
hay BD = 1/2 . AM
Hay AM = 2.BD ( đpcm )
c) Vì tam giác ABD = tam giác ACD ( cmt )
=> ^ADB = ^ADC ( hai góc tương ứng )
Mà ^ADB + ^ADC = 180o ( hai góc kề bù )
=> ^ADB = ^ADC = 180o/2 = 90o
=> AD vuông góc với BC (1)
Vì tam giác BEC = tam giác MEA ( cmt )
=> ^EBC = ^EMA ( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AM // BC (2)
Từ (1) và (2) => AM vuông góc với AD
=> ^MAD = 90o
# Học tốt #

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do dó: ABDC là hình bình hành
Suy ra: AB//DC
c: Xét ΔAED có
H là trung điểm của AE
M là trung điểm của AD
Do đó: HM là đường trung bình
=>HM//ED
=>ED\(\perp\)AE
Ta có: ΔAED vuông tại E
mà EM là đường trung tuyến
nên ME=MD

Hình bạn tự vẽ nha!
a) Xét 2 \(\Delta\) \(AMB\) và \(DMC\) có:
\(AM=DM\left(gt\right)\)
\(\widehat{AMB}=\widehat{DMC}\) (vì 2 góc đối đỉnh)
\(MB=MC\) (vì M là trung điểm của \(BC\))
=> \(\Delta AMB=\Delta DMC\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta AMB=\Delta DMC.\)
=> \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD.\)
Chúc bạn học tốt!


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)


a, Xét tam giác MAB và tam giác MDC có:
AM = MD
góc AMB = góc DMC
BM = CM
Nên: tam giác MAB = tam giác MDC
b, Ta có: tam giác MAB = tam giác MDC
=> góc ABM = góc DCM
Mà 2 góc này ở vị trí so le trong
Nên : AB//CD
c, Ta có: AB//CD
=> góc GAM = góc HDM( vì G∈ AB; H∈CD và 2 góc ở vị trí so le trong)
Xét tam giác GAM và tam giác HDM có:
AG = HD
góc GAM = góc HDM
AM = MD
Nên: tam giác GAM = tam giác HDM
=> GM = MH
Mà GM và MH có chung điểm M
=> MH và MG trùng nhau
Nên: 3 điểm G,H,M thẳng hàng
Cậu xem lại bài nhé, chúc cậu học tốt!!!
a) Xét 2 \(\Delta\) \(MAB\) và \(MDC\) có:
\(MA=MD\left(gt\right)\)
\(\widehat{AMB}=\widehat{DMC}\) (vì 2 góc đối đỉnh)
\(MB=MC\) (vì M là trung điểm của \(BC\))
=> \(\Delta MAB=\Delta MDC\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta MAB=\Delta MDC.\)
=> \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD.\)
c) Nối G với M, H với M.
Xét 2 \(\Delta\) \(AGM\) và \(DHM\) có:
\(AG=DH\left(gt\right)\)
\(\widehat{AMG}=\widehat{DMH}\) (vì 2 góc đối đỉnh)
\(AM=DM\left(gt\right)\)
=> \(\Delta AGM=\Delta DHM\left(c-g-c\right)\)
=> \(GM=HM\) (2 cạnh tương ứng).
Mà M nằm giữa G và H.
=> \(M\) là trung điểm của \(GH.\)
=> \(G,M,H\) thẳng hàng (đpcm).
Chúc bạn học tốt!