Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>BD//CA
c: Xét ΔABC và ΔDCB có
AB=DC
BC chung
AC=DB
=>ΔABC=ΔDCB
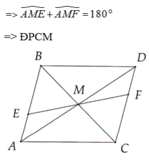
d: Xét tứ giác AEDF có
AE//DF
AE=DF
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng

a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD và AB//CD
b: Ta có: ABDC là hình bình hành
nên BD//AC
c: Ta có: AB//CD
nên \(\widehat{ABC}=\widehat{DCB}\)

a, Xét tam giác MAB và tam giác MDC có:
AM = MD
góc AMB = góc DMC
BM = CM
Nên: tam giác MAB = tam giác MDC
b, Ta có: tam giác MAB = tam giác MDC
=> góc ABM = góc DCM
Mà 2 góc này ở vị trí so le trong
Nên : AB//CD
c, Ta có: AB//CD
=> góc GAM = góc HDM( vì G∈ AB; H∈CD và 2 góc ở vị trí so le trong)
Xét tam giác GAM và tam giác HDM có:
AG = HD
góc GAM = góc HDM
AM = MD
Nên: tam giác GAM = tam giác HDM
=> GM = MH
Mà GM và MH có chung điểm M
=> MH và MG trùng nhau
Nên: 3 điểm G,H,M thẳng hàng
Cậu xem lại bài nhé, chúc cậu học tốt!!!
a) Xét 2 \(\Delta\) \(MAB\) và \(MDC\) có:
\(MA=MD\left(gt\right)\)
\(\widehat{AMB}=\widehat{DMC}\) (vì 2 góc đối đỉnh)
\(MB=MC\) (vì M là trung điểm của \(BC\))
=> \(\Delta MAB=\Delta MDC\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta MAB=\Delta MDC.\)
=> \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD.\)
c) Nối G với M, H với M.
Xét 2 \(\Delta\) \(AGM\) và \(DHM\) có:
\(AG=DH\left(gt\right)\)
\(\widehat{AMG}=\widehat{DMH}\) (vì 2 góc đối đỉnh)
\(AM=DM\left(gt\right)\)
=> \(\Delta AGM=\Delta DHM\left(c-g-c\right)\)
=> \(GM=HM\) (2 cạnh tương ứng).
Mà M nằm giữa G và H.
=> \(M\) là trung điểm của \(GH.\)
=> \(G,M,H\) thẳng hàng (đpcm).
Chúc bạn học tốt!

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC

c: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
\(\widehat{MBH}=\widehat{MCK}\)
Do đó; ΔMHB=ΔMKC
Suy ra: BH=CK
Xét tứ giác HBKC có
HB//KC
HB=KC
Do đó: HBKC là hình bình hành
SUy ra: HK và BC cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
hay H,M,K thẳng hàng

1 Xét 2 tam giác MAB và tam giác MDC:
Ta thấy:
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=MC (gt)
MA=MD (gt)
Từ các giả thiết trên, suy ra:
\(\Delta MAB=\Delta MDC\left(c-g-c\right)\)

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//DC