Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đo ba cạnh của tam giác vuông là \(x-d,x,x+d\)
Theo giả thiết ta có \(\left(x+d\right)^2=\left(x-d\right)^2+x^2\) (1)
Từ (1) tìm được \(x=0;x=4d\)
Như vậy có thể có tam giác vuông thỏa mãn đầu bài, các cạnh của nó là 3d, 4d, 5d. Đặc biệt, nếu \(d=1\) thì tam giác vuông có cách cạnh là 3, 4, 5 (tam giác Ai Cập)

Chọn C
Ba cạnh a, b, c ( a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa mãn yêu cầu thì:
a 2 + b 2 = c 2 a + b + c = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 3 b = 3 a + c = 2 b ⇔ a 2 + b 2 = c 2 b = 1 a = 2 b − c = 2 − c .
Ta có
a 2 + b 2 = c 2 → a = 2 − c b = 1 2 − c 2 + 1 = c 2
⇔ − 4 c + 5 = 0 ⇔ c = 5 4 ⇒ a = 3 4 b = 1 c = 5 4 .

Chọn C.
Gọi x, y, z theo thứ tự tăng dần của độ dài ba cạnh của tam giác.
Chu vi của tam giác: x + y + z = 3a (1)
Tính chất của cấp số cộng có x + z = 2y (2)
Vì tam giác vuông nên có: x2 + y2 = z2 (3)
Thay (2) vào (1) được 3y = 3a hay y = a, thay y = a vào (2) được: x + z = 2a hay x = 2a - z
Thay x và y vào (3) được: (2a – z)2 + a2 = z2 ⇔ 5a2 – 4az = 0 ⇔ 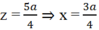
Độ dài ba cạnh của tam giác thỏa yêu cầu: 
Vậy độ dài cạnh lớn nhất của tam giác là ![]()

- Gọi độ dài các cạnh của đa giác trên là:\(a_1,a_2,...,a_n\left(cm\right)\left(a_1< a_2< ...< a_n\right)\left(n\in N\cdot,n>2\right)\)
- Vì độ dài các cạnh của đa giác trên lập thành 1 cấp số cộng nên ta có:
\(\left\{{}\begin{matrix}a_n=a_1+\left(n-1\right)d\\a_1+a_2+...+a_n=na_1+\dfrac{n\left(n-1\right)}{2}d\end{matrix}\right.\)
Mặt khác, theo đề bài ta có: \(\left\{{}\begin{matrix}a_n=15\left(cm\right)\\d=3\\a_1+a_2+...+a_n=45\left(cm\right)\end{matrix}\right.\)
Do đó: \(\left\{{}\begin{matrix}a_1+3\left(n-1\right)=15\left(1\right)\\na_1+\dfrac{3n\left(n-1\right)}{2}=45\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow na_1+3n\left(n-1\right)=15n\left(3\right)\)
Lấy \(\left(3\right)-\left(2\right)\), ta được: \(\dfrac{3n\left(n-1\right)}{2}=15n-45\)
\(\Leftrightarrow3n^2-3n+90-30n=0\)
\(\Leftrightarrow n^2-11n+30=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=6\\n=5\end{matrix}\right.\)
*Với \(n=6\). Từ (1) ta có: \(a_1=15-3\left(n-1\right)=15-3\left(6-1\right)=0\) (loại)
*Với \(n=5\). Từ (1) ta có: \(a_1=15-3\left(n-1\right)=15-3\left(5-1\right)=3\left(cm\right)\)
Vậy số cạnh của đa giác đó là 5.

Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).

Gọi 3 góc lần lượt là \(a;b;90\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=90\\2b=a+90\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=30\\b=60\end{matrix}\right.\)
Vậy số đo 3 góc là \(30^0;60^0;90^0\)

Chọn C
Giả sử ba cạnh của tam giác ABC là a,b,c. u 1 + u 1 q 4 = 51
không mất tính tổng quát, ta giả sử 0 < a≤a≤b≤c, nếu chúng tạo thành cấp số nhân thì theo tính chất của cấp số nhân Ta có: b2=ac.
Theo định lý hàm côsin Ta có:
![]()
![]()
Mặt khác a 2 + c 2 ≥ 2 a c ⇒ cos B ≥ 1 − 1 2
Vậy góc B ^ ≤ 60 ° ,mà a ≤ b ⇒ A ≤ 60 ° , cho nên tam giác ABC có hai góc không quá 60°

Chọn A.
Ta có ![]() và tam giác ABC nhọn nên A = 45º.
và tam giác ABC nhọn nên A = 45º.
A + B + C = 180 º ⇒ B + C = 180º - 45º = 135º
Do 3 góc tam giác lập thành cấp số cộng ; số đo góc A nhỏ nhất nên B = A + d; C = A + 2d.
Khi đó: B + C = A + d + A + 2d = 2A + 3d ⇒ 3d = 135º - 2.45º = 45º
⇒ d = 15º ⇒ B = A + d = 60º; C = A + 2d = 75º
Gọi số đo ba cạnh của tam giác vuông là x - d, x, x + d
Theo giả thiết ta có x + d 2 = x − d 2 + x 2 (1)
Từ (1) tìm được x = 0, x = 4d
Như vậy có thể có tam giác vuông thoả mãn đầu bài, các cạnh của nó là 3d, 4d, 5d. Đặc biệt, nếu d = 1 thì tam giác vuông có các cạnh là 3, 4, 5 (tam giác Ai Cập).