Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).

Chọn A.
Ta có ![]() và tam giác ABC nhọn nên A = 45º.
và tam giác ABC nhọn nên A = 45º.
A + B + C = 180 º ⇒ B + C = 180º - 45º = 135º
Do 3 góc tam giác lập thành cấp số cộng ; số đo góc A nhỏ nhất nên B = A + d; C = A + 2d.
Khi đó: B + C = A + d + A + 2d = 2A + 3d ⇒ 3d = 135º - 2.45º = 45º
⇒ d = 15º ⇒ B = A + d = 60º; C = A + 2d = 75º

Chọn C
Gọi số đo ba góc ba góc lập thành cấp số cộng là 25; 25+ d ; 25 +2d có công sai d.
Tổng ba góc trong một tam giác bằng 1800 nên :
u 1 + u 2 + u 3 = 180 ⇔ 25 + 25 + d + 25 + 2 d = 180 ⇔ 3 d = 105 ⇔ d = 35 .
Vâỵ
u 2 = 25 + 35 = 60 ; u 3 = 25 + 2 . 35 = 95.

Đặt \(u_1;u_2;u_3\) là 3 góc của tam giác lập thành cấp số nhân
Ta có :
\(u_1+u_2+u_3=180\)
\(\Leftrightarrow u_1+u_1.q+u_1.q^2=180\)
\(\Leftrightarrow u_1\left(1+q+q^2\right)=180\)
\(\Leftrightarrow u_1.13=180\)
\(\Leftrightarrow u_1=\dfrac{180}{13}\)
\(\Rightarrow\left\{{}\begin{matrix}u_2=3.\dfrac{180}{13}=\dfrac{540}{13}\\u_3=3^2.\dfrac{180}{13}=\dfrac{1620}{13}\end{matrix}\right.\)

Chọn A
Gọi d=2a là công sai. Bốn số phải tìm là:
A=(x-3a); B=(x-a); C=(x+a); D=(x+3a). Ta có hệ phương trình:
![]()
![]()

gọi a,b,c là 3 cạnh của tam giác.
Ta có :\(cot\left(\dfrac{A}{2}\right)+cot\left(\dfrac{C}{2}\right)=2cot\left(\dfrac{B}{2}\right)\) <=> \(\dfrac{cot\left(\dfrac{A}{2}\right)}{sin\left(\dfrac{A}{2}\right)}+\dfrac{cos\left(\dfrac{C}{2}\right)}{sin\left(\dfrac{C}{2}\right)}=\dfrac{2.cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\)
<=> \(\dfrac{sin\left(\dfrac{C}{2}\right)cos\left(\dfrac{A}{2}\right)+cos\left(\dfrac{C}{2}\right)sin\left(\dfrac{A}{2}\right)}{sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{C}{2}\right)}\)
<=> \(\dfrac{sin\left(\dfrac{A}{2}+\dfrac{C}{2}\right)}{sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\) <=> \(\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)}=2.\dfrac{cos\left(\dfrac{B}{2}\right)}{sin\left(\dfrac{B}{2}\right)}\)
<=> \(sin\left(\dfrac{B}{2}\right).cos\left(\dfrac{B}{2}\right)=2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)cos\left(\dfrac{B}{2}\right)\)
<=> \(\dfrac{1}{2}sinB=\left[cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)-cos\left(\dfrac{A}{2}+\dfrac{C}{2}\right)\right]cos\left(\dfrac{B}{2}\right)\)
<=>\(\dfrac{1}{2}sinB=cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right).cos\left(\dfrac{B}{2}\right)-sin\left(\dfrac{B}{2}\right)cos\left(\dfrac{B}{2}\right)\)
<=> \(\dfrac{1}{2}sinB=cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)sin\left(\dfrac{A}{2}+\dfrac{C}{2}\right)-\dfrac{1}{2}sinB\)
<=> sinB = \(\dfrac{1}{2}\left(sinA+sinC\right)\) <=> \(2sinB=sinA+sinC\)
<=> \(2.\dfrac{b}{2R}=\dfrac{a}{2R}+\dfrac{c}{2R}\)
<=> a+c =2b
=> 3 cạnh của tam giác tạo thành cấp số cộng.
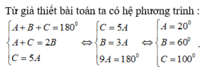
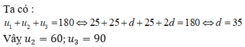
Gọi 3 góc lần lượt là \(a;b;90\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=90\\2b=a+90\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=30\\b=60\end{matrix}\right.\)
Vậy số đo 3 góc là \(30^0;60^0;90^0\)