
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

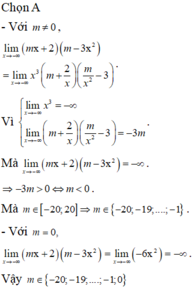

\(\lim\limits_{x\rightarrow-\infty}x^3\left(m+\dfrac{2}{x}\right)\left(\dfrac{m}{x^2}-3\right)=+\infty.\left(3m\right)=-\infty\)
\(\Rightarrow m< 0\Rightarrow\) có 20 giá trị nguyên của m
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]


\(f\left(x\right)=-x^3-2x^2+mx-3\)
\(f'\left(x\right)=-3x^2-4x+m\)
\(f'\left(x\right)>0\Leftrightarrow-3x^2-4x+m>0\Leftrightarrow m>3x^2+4x\)(đúng với mọi \(x\in\left(0,1\right)\))
suy ra \(m\ge max\left(3x^2+4x\right)\)với \(x\in\left[0,1\right]\).
Xét hàm \(g\left(x\right)=3x^2+4x\)với \(x\in\left[0,1\right]\).
\(g'\left(x\right)=6x+4\)
\(g'\left(x\right)=0\Leftrightarrow6x+4=0\Leftrightarrow x=-\frac{2}{3}\notin\left[0,1\right]\).
\(g\left(0\right)=0,g\left(1\right)=7\)
suy ra \(g_{max}=7\)
do đó \(m\ge7\).
Mà \(m\)nguyên, \(m\in\left[-2021,2021\right]\)nên có tổng cộng: \(2021-7+1=2015\)giá trị của \(m\)thỏa mãn.

a.
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2-ax+2021}-x+1\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(\sqrt{x^2-ax+2021}-x\right)\left(\sqrt{x^2-ax+2021}+x\right)}{\sqrt{x^2-ax+2021}+x}+1\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{-ax+2021}{\sqrt{x^2-ax+2021}+x}+1\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{x\left(-a+\dfrac{2021}{x}\right)}{x\left(\sqrt{1-\dfrac{a}{x}+\dfrac{2021}{x^2}}+1\right)}+1\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{-a+\dfrac{2021}{x}}{\sqrt{1-\dfrac{a}{x}+\dfrac{2021}{x^2}}+1}+1\right)\)
\(=\dfrac{-a+0}{\sqrt{1+0+0}+1}+1=-\dfrac{a}{2}+1\)
\(\Rightarrow a^2=-\dfrac{a}{2}+1\Rightarrow2a^2+a-2=0\)
Pt trên có 2 nghiệm pb nên có 2 giá trị a thỏa mãn
b.
\(\lim\limits_{x\rightarrow-1}f\left(x\right)=\lim\limits_{x\rightarrow-1}\dfrac{x^3+1}{x+1}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{x+1}=\lim\limits_{x\rightarrow-1}\left(x^2-x+1\right)\)
\(=1+1+1=3\)
\(f\left(-1\right)=3a\)
Hàm gián đoạn tại điểm \(x_0=-1\) khi:
\(\lim\limits_{x\rightarrow-1}f\left(x\right)\ne f\left(-1\right)\Rightarrow3\ne3a\)
\(\Rightarrow a\ne1\)

1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số