Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó
C
1
,
C
2
, C là ba tập con không giao nhau của S và S =
C
1
∪
C
2
∪
C
Khi đó mỗi phần tử x ∈ S có 3 khả năng: Hoặc thuộc tập C 1 hoặc thuộc tập C 2 hoặc thuộc tập C.
Do đó 12 phần tử sẽ có 3 12 cách chọn.
Trong các cách chọn nói trên có 1 trường hợp C 1 = C 2 = ∅ , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò C 1 và C 2 cho nhau).
Do đó số cách chia là 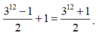
Cách 2.
Đặt S = S 1 ∪ S 2
Nếu
S
1
có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 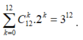
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có  cách
cách

[Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = [Số cách chọn 4 em trong 12 em] - [số cách chọn mà mỗi lớp có ít nhất 1 em]
Mà:
[Số cách chọn 4 em trong 12 em] = \(C^4_{12}=\frac{12!}{4!\left(12-4\right)!}=495\)
[số cách chọn mà mỗi lớp có ít nhất 1 em] = [Số cách chọn lớp A có 2 hs, lớp B, C mỗi lớp có 1 hs] + [Số cách chọn lớp B có 2 hs, lớp A, C mỗi lớp có 1 hs] + [Số cách chọn lớp C có 2 hs, lớp A, B mỗi lớp có 1 hs]
= \(C^2_5.C^1_4.C^1_3+C^1_5.C^2_4.C^1_3+C^1_5.C^1_4.C^2_3\)
= 120 + 90 + 60
= 270
Vậy [Số cách chọn 4 em sao cho thuộc không quá 2 trong 3 lớp] = 495 - 270 =....

a/ \(C_{12}^3\)
b/ \(\frac{C_3^3+C_4^3+C_5^3}{C_{12}^3}\)
c/ \(\frac{C_4^3+C_4^2.C_8^1}{C_{12}^3}\)
d/ Có 3 cách lấy 1 tấm thẻ xanh, 3 cách để lấy thẻ đỏ khác số với thẻ xanh và 3 cách để lấy thẻ vàng khác số với 2 thẻ trước đó
Vậy có \(3.3.3\) cách lấy
Xác suất: \(\frac{3.3.3}{C_{12}^3}\)

Đáp án B
n ( Ω ) = C 12 4
Gọi H:” Không có quá 2 trong 3 lớp”
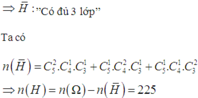

Khi các hệ số tùy ý; ta cần thực hiện các bước sau:
Chọn hệ số a: có 4 cách chọn hệ số a vì a≠0.
Chọn hệ số b: có 5 cách chọn hệ số b.
Chọn hệ số c: có 5 cách chọn hệ số c
Chọn hệ số d: có 5 cách chọn hệ số d.
Theo quy tắc nhân có: 4.5.5.5=500 đa thức.
Chọn C.



Đáp án D