Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 3A = 3.(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−1
⇒ A = 3101−1
2
Vậy A = 3101−1
2

B = 31 + 32 + 33 +...+ 3100
3B = 32 + 33 + ...+ 3100 + 3101
3B - B = 3101 - 3
2B = 3101 - 3
2B + 3 = 3n
⇒ 3101 - 3 + 3= 3n
3n = 3101
n = 101
Kết luận n = 101

A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101

Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101



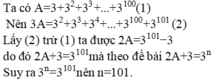
1, Số có tận cùng là 3 khi nâng lên lũy thừa 4n sẽ có tận cùng là 1
Do đó: \(43^{43}=43^{4.10+3}=\left(....1\right).\left(...7\right)=\left(...7\right)\)
Số có tận cùng là 7 khi nâng lên lũy thừa 4n sẽ có tận cùng là 1
Do đó: \(17^{17}=17^{4.4+1}=\left(.....1\right).\left(...7\right)=\left(...7\right)\)
\(\Rightarrow43^{43}-17^{17}=\left(...7\right)-\left(....7\right)=\left(....0\right)\)
Số có tận cùng là 0 thì chia hết cho 5
\(\Rightarrow43^{43}-17^{17}⋮5\)
2. Tổng các chữ số của \(100^{1995}\)là:
1+0+0+....+0=1
\(\Rightarrow\)Tổng các chữ số của \(100^{1995}\)và 8 là:
1+8=9 \(⋮\)9
\(\Rightarrow\left(100^{1995}+8\right)⋮9\)
Vậy \(\frac{100^{1995}+8}{9}\)là số tự nhiên
3, \(3+3^2+3^3+....+3^{100}\)
\(=\left(3+3^2+3^3+3^4\right)+....+\left(3^{96}+3^{97}+3^{98}+3^{99}\right)\)
\(=3\left(1+3+3^2+3^3\right)+....+3^{96}\left(1+3+3^2+3^3\right)\)
\(=40\left(3+3^5+...+3^{96}\right)\)
\(\Rightarrow\left(3+3^2+3^3+....+3^{100}\right)⋮40\)(vì có chứa thừa số 40)