Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}SM\perp\left(MNPQ\right)\Rightarrow SM\perp PN\\PN\perp MN\end{matrix}\right.\) \(\Rightarrow PN\perp\left(SMN\right)\)
Lại có \(\left\{{}\begin{matrix}PN\perp\left(SMN\right)\\SN\in\left(SMN\right)\end{matrix}\right.\) \(\Rightarrow PN\perp SN\)

- Khi n = 1, VT = 1;
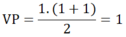
⇒ VT = VP , do đó đẳng thức đúng với n = 1.
- Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
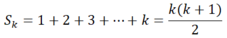
Ta phải chứng minh rằng đẳng thức cũng đúng với n = k + 1, tức là:
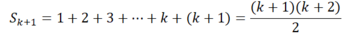
Thật vậy, từ giả thiết quy nạp ta có:
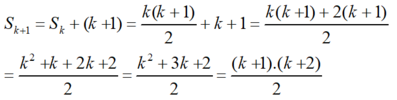
Vậy đẳng thức đúng với mọi n ∈ N*


Do 2 + 1 chia hết cho 3 nên theo bổ đề LTE ta có \(v_3\left(2^{3^n}+1\right)=v_3\left(2+1\right)+v_3\left(3^n\right)=n+1\).
Do đó \(2^{3^n}+1⋮3^{n+1}\) nhưng không chia hết cho \(3^{n+2}\).

- Với \(n=4\Rightarrow3^3>4.6\) (đúng)
- Giả sử BĐT đã cho đúng với \(n=k\ge4\) hay \(3^{k-1}>k\left(k+2\right)\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay: \(3^k>\left(k+1\right)\left(k+3\right)\)
Thật vậy, do \(k\ge4\Rightarrow k-3>0\), ta có:
\(3^k=3.3^{k-1}>3k\left(k+2\right)=3k^2+6k=\left(k^2+4k+3\right)+\left(2k^2+2k-3\right)\)
\(=\left(k+1\right)\left(k+3\right)+2k^2+k+\left(k-3\right)>\left(k+1\right)\left(k+3\right)\) (đpcm)

Tham Khảo:
a) Gọi d là công sai của cấp số cộng (un) ,d ≠ 0. Khi đó với mọi n ∈ N*, ta có:
Pn + 1 - pn = 4(un+ 1 - un) = 4d (không đổi )
Vậy (pn) là cấp số cộng
Sn + 1 - Sn = (un+1 - un)(un+1 + un) = d(un+1 + un)
không là hằng số( do d ≠ 0)
Vậy (Sn)không là cấp số cộng.
b)
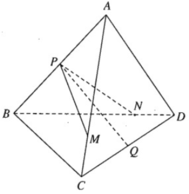
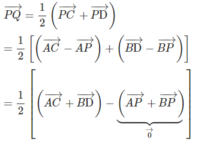
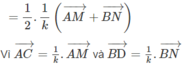
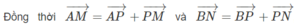
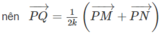
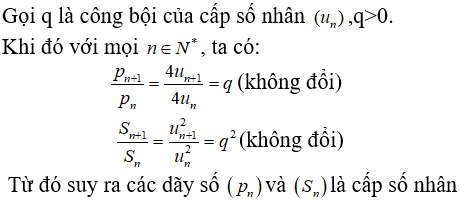
- Với \(n=2\Rightarrow P_2=2!=2=1!+1\) (đúng)
- Với \(n=3\Rightarrow\left\{{}\begin{matrix}P_3=3!=6\\2P_2+P_1+1=2.2!+1+1=6\end{matrix}\right.\) (đúng)
- Giả sử đẳng thức đúng với \(n=k\ge2\) hay:
\(P_k=\left(k-1\right)P_{k-1}+\left(k-2\right)P_{k-2}+...+P_1+1\)
Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay
\(P_{k+1}=k.P_k+\left(k-1\right)P_{k-1}+...+P_1+1\)
Thật vậy, ta có:
\(k.P_k+\left(k-1\right)P_{k-1}+...+P_1+1=k.P_k+P_k\)
\(=\left(k+1\right)P_k=P_{k+1}\) (đpcm)