K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
1
TV
23 tháng 11 2017
Đặt A là tổng của 2^1 + 2^2 + 2^3 +.....+ 2^88 +2^89 + 2^90
= (2^1 + 2^2 + 2^3) + ....+ (2^88 + 2^89 +2^90)
= (2^1.1+2^1.2+2^1.2^2) +....+(2^88.1+2^88.2+2^88.2^2)
= 2^1.(1+2+2^2) +.....+2^88.(1+2+2^2)
= 2^1.7 +....+2^88.7
= 7.(2^1+....+2^88)
=> A chia hết cho 7
8 tháng 12 2023
\(8^8+2^{20}\)
\(=\left(2^3\right)^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)\)
\(=2^{20}\cdot17⋮17\)
HN
0
CM
12 tháng 8 2017
Sơ đồ con đường |
Lời giải chi tiết |
|
Xét 5 3 . 5 2 − 5 + 1 = 5 3 .21 Áp dụng tính chất chia hết của một tích: 21 ⋮ 7 ⇒ 5 3 .21 ⋮ 7 ⇒ 5 3 . 5 2 − 5 + 1 ⋮ 7 ⇒ 5 5 − 5 4 + 5 3 ⋮ 7 |
HT
1
TL
2
21 tháng 7 2016
Ta có:
4141/8888 = 41×101/88×101 = 41/88
414141/888888 = 41×10101/88×10101 = 41/88
=> đpcm
21 tháng 7 2016
+) 414141/888888=414141:10101/888888:10101=41/88
+) 4141/8888=4141:101/8888:101=41/88
Ta thay : 41/88 =41/88 =41/88
Suy ra: 414141/888888=4141/8888=41/88
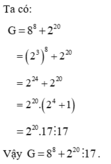
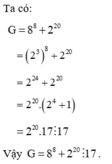
810 - 89 - 88 =88 (82 -8-1)=88 x 55 chia hết cho 55
810-89-88
= 88.(82-8-1)
= 88.(64-8-1)
= 88.55 ⋮ 55