Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

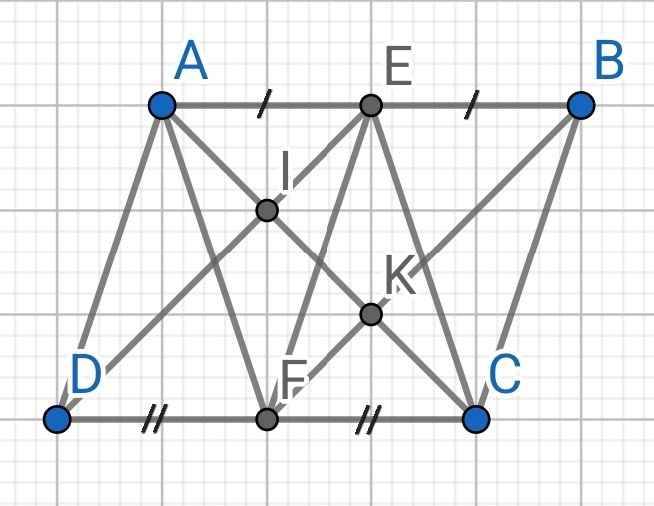 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

a: Xét tứ giác EBDA có
EB//DA
EA//DB
Do đó: EBDA là hình bình hành
Xét tứ giác ABDF có
AB//DF
AF//BD
Do đó: ABDF là hình bình hành

a) Vì BD là phân giác của \(\widehat{ABC}\) nên \(\widehat{ABD}=\widehat{DBC}=\frac{1}{2}\widehat{ABC}\)
Lại có \(\widehat{EBD}=\widehat{EDB}\)(gt)
=> \(\widehat{EDB}=\widehat{DBC}\)
Mà 2 góc ở vị trí so le trong nên ED//BC
Chúc bạn làm bài tốt!!!!
b) Vì ED//BC nên \(\widehat{AED}=\widehat{ABC}\)(đồng vị) (1)
Vì EF//BD nên \(\widehat{AEF}=\widehat{ABD}\)(đồng vị) (2)
Lại có \(\widehat{ABD}=\frac{1}{2}\widehat{ABC}\)(cmt) (3)
Từ (1),(2) và (3) suy ra \(\widehat{AEF}=\frac{1}{2}\widehat{AED}\)
=> EF là tia phân giác của góc AED
Chúc bạn làm bài tốt !!!!!!!!!!

a,
ABCD là hình thang cân \(=>\angle\left(CAB\right)=\angle\left(DBA\right)\)
=>2 góc ngoài cũng bằng nhau
=>2 tia phân giác 2 góc ngoài cũng tạo thành các góc bằng nhau
\(=>\angle\left(EAB\right)=\angle\left(FBA\right)\)=>ABFE là hình thang cân
b,từ 2 điểm A,B hạ các đường cao AM,BN
chứng minh được AMNB là h chữ nhật
=>MN=AB=6cm
dễ chứng minh được tam giác ADM=tam giác BCN(ch-cgn)
\(=>DM=CN=\dfrac{1}{2}\left(DC-MN\right)=\dfrac{1}{2}\left(12-6\right)=3cm\)
pytago=>\(BN=\sqrt{BC^2-NC^2}=\sqrt{5^2-3^2}=4cm\)
\(=>SABCD=\dfrac{BN\left(AB+CD\right)}{2}=........\)thay số tính
Tứ giác \(ABCD\) là hình bình hành
=> \(\widehat{ADC}=\widehat{ABC}\)
Lại có: `\(\)BF, DE` lần lượt là phân giác của \(\widehat{ABC}\) và \(\widehat{ADC}\)
=> \(\widehat{ADE}=\widehat{EDC}=\widehat{ABF}=\widehat{FBC}\)
Mà `AB` // `DC =>` \(\widehat{ABF}=\widehat{BFC}\) (2 góc so le trong)
=> \(\widehat{EDC}=\widehat{BFC}\)
Mà 2 góc đó là 2 góc đồng vị
`=> DE` // `BF` (đpcm)