Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sủa đề : CM \(A=\frac{2ax-2x-3y+3ay}{4ax+4x+6y+6ay}\) ko phụ thuộc vào biếnx;y :
Ta có : \(\frac{2ax-2x-3y+3ay}{4ax+4x+6y+6xy}=\frac{a\left(2x+3y\right)-\left(2x+3y\right)}{2a\left(2x+3y\right)+2\left(2x+3y\right)}=\frac{\left(a-1\right)\left(2x+3y\right)}{\left(2a+2\right)\left(2x+3y\right)}=\frac{a-1}{2a+2}\)
Biểu thức sau khi dút gọn ko chứa biến của x;y nên A ko phụ thuộc vào biến x;y (đpcm)

a) \(\frac{\left(x+a\right)^2-x^2}{2x+a}=\frac{x^2+2xa+a^2-x^2}{2x+a}=\frac{2ax+a^2}{2x+a}=\frac{a\left(2x+a\right)}{2x+a}=a\)
b) \(\frac{x^2-y^2}{axy-ax^2-ay^2-axy}=\frac{x^2-y^2}{-a\left(x^2+y^2\right)}\) =>cần phụ thuộc vào x,y (Không thì đề sai)
c) \(\frac{2ax-2x-3y+3ay}{4ax+6x+9y+6ay}=\frac{2x\left(a-1\right)+3y\left(a-1\right)}{2x\left(a+3\right)+3y\left(a+3\right)}=\frac{\left(2x+3y\right)\left(a-1\right)}{\left(2x+3y\right)\left(a+3\right)}=\frac{a-1}{a+3}\)
Bạn xem đề câu b và c nhé..... C tớ có sửa rồi nhưng không biết đúng hay sai


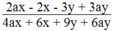 xác định khi 4ax + 6x + 9y + 6ay
≠
0
xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
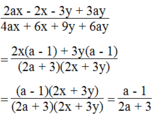
Vậy biểu thức không phụ thuộc vào x, y.

a) \(\frac{x^2-y^2}{\left(x+y\right)\left(ay-\text{ax}\right)}=\frac{\left(x+y\right)\left(x-y\right)}{-a\left(x+y\right)\left(x-y\right)}=\frac{-1}{a}\)
b) \(\frac{2ax-2x-3y+3ay}{4ax+\text{4x}+6y+6ay}=\frac{2x\left(a-1\right)+3y\left(a-1\right)}{\text{4x}\left(a+1\right)+6y\left(a+1\right)}\)
\(=\frac{\left(a-1\right)\left(2x+3y\right)}{2\left(a+1\right)\left(2x+3y\right)}=\frac{a-1}{2\left(a+1\right)}\)

bài 1)
a) \(\dfrac{2ax-2x-3y+3ay}{4ax+6x+9y+6ay}\)
= \(\dfrac{\left(2ax-2x\right)+\left(3ay-3y\right)}{\left(4ax+6x\right)+\left(6ay+9y\right)}\)
= \(\dfrac{2x\left(a-1\right)+3y\left(a-1\right)}{2x\left(2a+3\right)+3y\left(2a+3\right)}\)
= \(\dfrac{\left(2x+3y\right)\left(a-1\right)}{\left(2x+3y\right)\left(2a+3\right)}\)
= \(\dfrac{a-1}{2a+3}\)
Vậy biểu thức \(\dfrac{2ax-2x-3y+3ay}{4ax+6x+9y+6ay}\) ko phụ thuộc vào biến x,y mà phụ thuộc vào biến a

Ps : mình nghĩ đề bài sai rồi, phải là rút gọn biểu thức
a, \(-\frac{2}{3}xy^2\left(x^2-x+6y^2-3y^3\right)=-\frac{2x^3y^2}{3}+\frac{2x^2y^2}{3}-4xy^4+3xy^5\)
Vậy biểu thức phụ thuộc biến x
b, \(\left(12x-5y\right)\left(2x-y+10\right)=24x^2-12xy+120x-10xy+5y^2-50y\)
\(=24x^2-22xy+120x+5y^2-50y\)
Vậy biểu thức phụ thuộc biến x

Bài \(3\)
\(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-\left(2x^2-6x\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
\(=\left(2x^2-2x^2\right)+\left(3x-10x+6x+x\right)+\left(-15+7\right)\)
\(=-8\)
Vậy biểu thức không phụ thuộc vào biến
\(B=4\left(y-6\right)-y^2\left(2+3y\right)+y\left(5y-4\right)+3y^2\)
Đề như này à?
Bài \(4\)
\(a,4a^2-16b^2=4\left(a^2-4b^2\right)=4\left(a-2b\right)\left(a+2b\right)\)
\(b,4x^2-4x+1=\left(2x\right)^2-2.2x.1+1^2=\left(2x+1\right)^2\)
\(c,\) ?
\(d,\left(x-y\right)^2-\left(2x-y\right)^2\\ =\left[\left(x-y\right)-\left(2x-y\right)\right]\left[\left(x-y\right)+\left(2x-y\right)\right]\\ =\left(x-y-2x+y\right)\left(x-y+2x-y\right)\\ =\left(-x\right)\left(3x-2y\right)\)
\(e,8x^3-y^3=\left(2x\right)^3-y^3\\ =\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(i,3x+6y+\left(x+2y\right)\\ =3\left(x+2y\right)+\left(x+2y\right)\\ =4\left(x+2y\right)\)
\(j,ax-ay-x+y=\left(ãx-ay\right)-\left(x-y\right)\\ =a\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(a-1\right)\)
`k,` `y` hay `y^2` ạ? vì nó mới phân tích được nhân tử.

a) Ta có : \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) = \(\frac{(x-y)(x+y)}{(x+y).a(y-x)}\)
= \(\frac{(x-y)(x+y)}{-a(x-y)(x+y)}\)
= \(\frac{-1}{a}\)
Vì \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) = \(\frac{-1}{a}\) Nên giá trị của \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) không phụ thuộc vào biến x
b) Xem lại đề bài nhé Đề bài sai chăng ?!
Đề bài sai chăng ?!