Chứng minh 1 3 ≤ x 2 − x + 1 x 2 + x...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

11 tháng 11 2019

Chứng minh 1 3 ≤ x 2 − x + 1 x 2 + x + 1 ≤ 3 với mọi giá trị của x.

#Toán lớp 8

Cao Minh Tâm

11 tháng 11 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Kagamine Len

17 tháng 12 2019 - olm

1) chứng minh biểu thức sau là 1 số nguyên tố với mọi giá trị của m : A = ( x - 1 ) ² - ( m² + 1 ) ( m - 3 )²- 2m

2) Thực hiện phép chia sau : ( x² - 2x - y² + 1 ) : ( x - y - 1 )

3) chứng minh cho giá trị của biểu thức P = x - x² - 1 luôn âm với mọi giá trị của x

#Toán lớp 8

tai tui

5 tháng 11 2021

cho biểu thức A = ( x - 3 ) ( x2 + 3x + 9 ) - ( x - 1 )3 + 4 ( x + 2 ) ( 2 - x ) - x

a. Chứng minh A = - x2 - 4x - 10

b. Chứng minh A luôn có giá trị âm với mọi giá trị của số thực x

#Toán lớp 8

Nguyễn Lê Phước Thịnh

5 tháng 11 2021

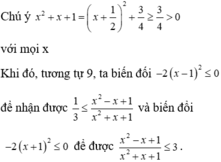
a: \(A=x^3-27-x^3+3x^2-3x+1-4\left(x^2-4\right)-x\)

\(=3x^2-4x-26-4x^2+16\)

\(=-x^2-4x-10\)

Đúng(0)

Phạm Mèo Mun

5 tháng 2 2020 - olm

a) Với giá trị nào của x thì giá trị biểu thức -1 / 4x + 2 < 0
b) Chứng minh biểu thức -x^2 - 2x - 3 / x^2 + 1 < 0 với mọi x

#Toán lớp 8

Lê Tài Bảo Châu

5 tháng 2 2020

a)\(\frac{-1}{4x+2}< 0\)

\(\Leftrightarrow4x+2>0\)

\(\Leftrightarrow4x>-2\)

\(\Leftrightarrow x>\frac{-1}{2}\)

Vậy ...

b)\(\frac{-x^2-2x-3}{x^2+1}\)

Ta có: \(-x^2-2x-3=-\left(x+1\right)^2-2\)

Vì \(-\left(x+1\right)^2\le0;\forall x\)

\(\Rightarrow-\left(x+1\right)^2-2\le-2< 0;\forall x\)

Lại có \(x^2\ge0;\forall x\)

\(\Rightarrow x^2+1\ge1>0;\forall x\)

\(\Rightarrow\frac{-x^2-2x-3}{x^2+1}< 0;\forall x\)

Đúng(0)

Lý Vũ Thị

25 tháng 7 2023

Cho phân thức: A=(3-6x)/(2x^3-x^2+2x-1) a) Rút gọn phân thức. b) Tính giá trị của phân thức tại x=3. c) Chứng minh A luôn âm với mọi giá trị của x khác 1/2.

#Toán lớp 8

Nguyễn Lê Phước Thịnh

25 tháng 7 2023

a: \(A=\dfrac{3\left(1-2x\right)}{2x\left(x^2+1\right)-\left(x^2+1\right)}\)

\(=\dfrac{-3\left(2x-1\right)}{\left(x^2+1\right)\left(2x-1\right)}=\dfrac{-3}{x^2+1}\)

b: Khi x=3 thì \(A=\dfrac{-3}{3^2+1}=-\dfrac{3}{10}\)

c: x^2+1>=0

=>3/x^2+1>=0

=>-3/x^2+1<=0

=>A<=0(ĐPCM)

Đúng(1)

Soái muội

23 tháng 11 2019 - olm

a) Tìm giá trị nhỏ nhất của biểu thức: A=x^2+3x-5

b) Chứng minh rằng A(x)=1/120x^5 -1/24 x^4+1/14x^3+1/24x^2-1/20x nhận giá trị nguyên với mọi giá trị nguyên của x

#Toán lớp 8

Kiệt Nguyễn

23 tháng 11 2019

\(A=x^2+3x-5=x^2+3x+\frac{9}{4}-\frac{29}{4}\)

\(=\left(x+\frac{3}{2}\right)^2-\frac{29}{4}\ge-\frac{29}{4}\)

Vậy \(A_{min}=-\frac{29}{4}\Leftrightarrow x+\frac{3}{2}=0\Leftrightarrow x=-\frac{3}{2}\)

Đúng(0)

Tran An Ngan

9 tháng 9 2016 - olm

Cho A= (x^2+1)^4+ 9(x^2+1)^3+ 21(x^2+1)^2- x^2-31. Chứng minh rằng A luôn luôn không âm với mọi giá trị của biến.

#Toán lớp 8

Quận Hoàng Đăng

10 tháng 9 2016

co gi pm nha buon ngu qua

Đúng(0)

☆MĭηɦღAηɦ❄

3 tháng 8 2020

\(A=\left(x^2+1\right)^4+9\left(x^2+1\right)^3+21\left(x^2+1\right)^2-\left(x^2+1\right)-30\)

Ta thấy \(x^2+1\ge1>0\forall x\)

\(\Rightarrow\left(x^2+1\right)^2\ge\left(x^2+1\right)\forall x\ge0\)

\(\Leftrightarrow\left(x^2+1\right)^2-\left(x^2+1\right)\ge0\)

\(\Rightarrow A=\left(x^2+1\right)^4+9\left(x^2+1\right)^3+20\left(x^2+1\right)^2+\left(x^2+1\right)^2-\left(x^2+1\right)-30\)

\(\ge1^4+9.1^4+20.1^2+0-30=0\)

\(\Rightarrow Min.A=0\Leftrightarrow x^2+1=1\Leftrightarrow x=0\)

Vậy A luôn không âm với mọi giá trị của biến.

Đúng(0)

shoppe pi pi pi pi

8 tháng 10 2018 - olm

a/chứng minh rằng biểu thức sau không âm với mọi giá trị của biến
A=(-15.x^3.y^6):(-5xy^2)
b/chứng minh rằng giá trị biểu thức sau ko phụ thuộc vào giá trị của biến y(x,y khác 0)
B=2/3 x^2 y^3:(-1/3xy)+2x(y-1)(y+1)

#Toán lớp 8