Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(abc=2\)nên ta có:
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)
\(=\frac{1+b+bc}{bc+c+1}=1\)

thế abc=2 vào M ta có
M=\(\frac{a}{ab+b+abc}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac+abc^2+abc}\)
M=\(\frac{a}{a\left(bc+b+1\right)}\)+\(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac\left(bc+b+1\right)}\)
M=\(\frac{bc+b+1}{bc+b+1}\)=1
1 nha bạn cho mình nha

Nhận xét: \(b^3c-cb^3=0;b^2c-cb^2=0.\).Nên phân thức trở thành:
\(\frac{a^3b-ab^3+c^3a-ca^3}{a^2b-ab^2+c^2a-ca^2}=\frac{a^3\left(b-c\right)-a\left(b^3-c^3\right)}{a^2\left(b-c\right)-a\left(b^2-c^2\right)}\)
\(=\frac{a\left(b-c\right)\left\{a^2-\left(b^2-bc+c^2\right)\right\}}{a\left(b-c\right)\left\{a-\left(b+c\right)\right\}}\)
\(=\frac{a^2-\left(b^2-bc+c^2\right)}{a-\left(b+c\right)}=\frac{a^2-\left(b+c\right)^2+3bc}{a-\left(b+c\right)}\)
\(=a+b+c+\frac{3bc}{a-b-c}\).

\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{abc+2bc+2b}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1+b+bc}{b+1+bc}=1\)
Vậy \(M=1.\)

b, \(B=\frac{\frac{x}{x+3}-\frac{9}{x^2+6x+9}}{\frac{3}{x+3}}=\frac{\frac{x}{x+3}-\frac{3^2}{x^2+2\cdot3\cdot x+3^2}}{\frac{3}{x+3}}\)
\(=\frac{\frac{x}{x+3}-\left(\frac{3}{x+3}\right)^2}{\frac{3}{x+3}}=1-\frac{3}{x+3}\)
a, Vậy điều kiện là \(x\ne3\)
c, \(B=\frac{1}{3}\Leftrightarrow1-\frac{3}{x+3}=\frac{1}{3}\)
\(\Rightarrow\frac{3}{x+3}=\frac{2}{3}\Leftrightarrow x=\frac{3}{2}\)

Ta có ; \(\frac{a}{ab+a+2}\)+\(\frac{b}{bc+b+1}\)+\(\frac{c}{ac+2c+2}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{abc+ab+a}\)+\(\frac{c}{ac+2c+abc}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{c}{c\left(a+2+ab\right)}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{1}{a+ab+2}\)
=\(\frac{a+ab+1}{ab+a+2}\)
Đề bài này hình như có gì sai bạn ạ
đáng ra phải là \(\frac{2c}{ac+2c+2}\) chứ
À xin lỗi nha mình nhập sai. đúng là : \(\frac{2c}{ac+2c+2}\)

\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{b+1+bc}+\frac{2c}{c\left(a+ab+2\right)}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{2}{a+2+ab}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{bc}{b+bc+1}\)
\(=\frac{b+bc+1}{b+bc+1}=1\)
Theo bài ra , ta có :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(\Leftrightarrow\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2bc}{b\left(ac+2c+2\right)}\)(Vì abc = 2 )
\(\Leftrightarrow\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{abc+2bc+2b}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)( Vì abc = 2 )
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}\)
\(\Leftrightarrow\frac{1+b+bc}{b+1+bc}=1\)
Vậy M=1
Chúc bạn học tốt =))![]()
Phan Cả Phát xin hết !!!

cho mình xửa lại một chút nha:tính : A=\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ca+2c+2}\)
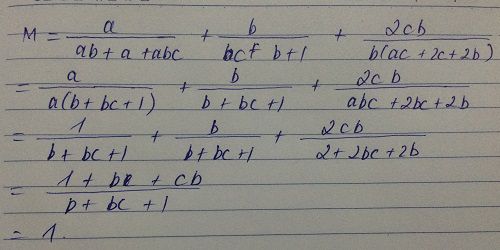
thay 2=abc mà giải bạn nhé