Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(abc=2\)nên ta có:
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc.c}{ac+abc.c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+c+1}\)
\(=\frac{1+b+bc}{bc+c+1}=1\)

thế abc=2 vào M ta có
M=\(\frac{a}{ab+b+abc}\)+ \(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac+abc^2+abc}\)
M=\(\frac{a}{a\left(bc+b+1\right)}\)+\(\frac{b}{bc+b+1}\)+ \(\frac{abc^2}{ac\left(bc+b+1\right)}\)
M=\(\frac{bc+b+1}{bc+b+1}\)=1
1 nha bạn cho mình nha

\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+abc}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{b+1+bc}+\frac{2c}{c\left(a+ab+2\right)}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{2}{a+2+ab}\)
\(=\frac{1}{b+bc+1}+\frac{b}{b+bc+1}+\frac{bc}{b+bc+1}\)
\(=\frac{b+bc+1}{b+bc+1}=1\)
Theo bài ra , ta có :
\(M=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(\Leftrightarrow\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2bc}{b\left(ac+2c+2\right)}\)(Vì abc = 2 )
\(\Leftrightarrow\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{abc+2bc+2b}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)( Vì abc = 2 )
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(\Leftrightarrow\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{bc}{1+bc+b}\)
\(\Leftrightarrow\frac{1+b+bc}{b+1+bc}=1\)
Vậy M=1
Chúc bạn học tốt =))![]()
Phan Cả Phát xin hết !!!

Ta có ; \(\frac{a}{ab+a+2}\)+\(\frac{b}{bc+b+1}\)+\(\frac{c}{ac+2c+2}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{abc+ab+a}\)+\(\frac{c}{ac+2c+abc}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{c}{c\left(a+2+ab\right)}\)
=\(\frac{a}{ab+a+2}\)+\(\frac{ab}{a+ab+2}\)+\(\frac{1}{a+ab+2}\)
=\(\frac{a+ab+1}{ab+a+2}\)
Đề bài này hình như có gì sai bạn ạ
đáng ra phải là \(\frac{2c}{ac+2c+2}\) chứ
À xin lỗi nha mình nhập sai. đúng là : \(\frac{2c}{ac+2c+2}\)

\(M=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2c}{abc+2bc+2b}\)
\(=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2bc}{2+2bc+2b}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2bc}{2\left(1+bc+b\right)}\)
\(=\frac{1+b+bc}{b+1+bc}=1\)
Vậy \(M=1.\)

a) \(\frac{4x^2-3x+17}{x^3-1}+\frac{2x-1}{x^2+x+1}+\frac{6}{1-x}\)
\(=\frac{4x^2-3x+17}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{\left(x-1\right)\left(2x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{6\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{4x^2-3x+17+2x^2-x-2x+1-6x^2-6x-6}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{-12x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{-12\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=-\frac{12}{x^2+x+1}\)
b) \(\frac{1}{x^2-x+1}-\frac{x^2+2}{x^3+1}+1=\frac{x+1-x^2-2+x^3+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x-x^2+x^3}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{x\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{x}{x+1}\)
c) \(N=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{2017c}{ac+2017c+2017}\)
\(N=\frac{a}{a\left(b+1+bc\right)}+\frac{b}{bc+b+1}+\frac{2017c}{ac+2017c+2017}\)
\(N=\frac{1}{b+1+bc}+\frac{b}{bc+b+1}+\frac{2017c}{ac+2017c+2017}\)
\(N=\frac{1+b}{b+1+bc}+\frac{abc^2}{ac+abc^2+abc}\)
\(N=\frac{1+b}{b+1+bc}+\frac{abc^2}{ac\left(1+bc+b\right)}\)
\(N=\frac{1+b}{b+1+bc}+\frac{bc}{1+bc+b}\)
\(N=\frac{1+b+bc}{b+1+bc}\)
\(N=1.\)

\(M=\frac{b}{bc+b+1}+\frac{a}{ab+a+2}+\frac{2c}{ac+2c+2}\)
\(=\frac{b}{bc+b+1}+\frac{a}{ab+a+abc}+\frac{abc^2}{ac+abc^2+abc}\)
\(=\frac{b}{bc+b+1}+\frac{a}{a\left(bc+b+1\right)}+\frac{abc^2}{ac\left(bc+b+1\right)}\)
\(=\frac{b}{bc+b+1}+\frac{1}{bc+b+1}+\frac{bc}{bc+b+1}\)
\(=\frac{bc+b+1}{bc+b+1}=1\)
Vậy M = 1
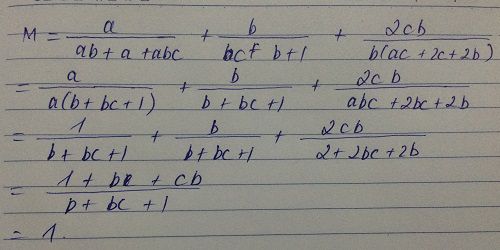
cho mình xửa lại một chút nha:tính : A=\(\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ca+2c+2}\)