Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay tọa độ A vào ta được: \(\dfrac{b}{-1}=-1\Rightarrow b=1\)
\(\Rightarrow y=\dfrac{ax+1}{x-1}\Rightarrow y'=\dfrac{-a-1}{\left(x-1\right)^2}\)
\(y'\left(0\right)=-3\Leftrightarrow\dfrac{-a-1}{\left(0-1\right)^2}=-3\Leftrightarrow-a-1=-3\)
\(\Rightarrow a=2\)

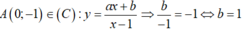
- Ta có: 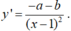
- Hệ số góc của tiếp tuyến với đồ thị tại điểm A là: k = y'(0)
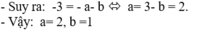
Chọn B.

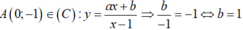
- Ta có: 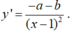
- Hệ số góc của tiếp tuyến với đồ thị tại điểm A là: k = y'(0)
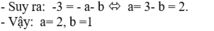
Chọn B.

a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)

\(y'=3x^2-6x\)
Do M thuộc (C) nên hệ số góc của tiếp tuyến tại M:
\(k=f\left(a\right)=3a^2-6a\)
\(f'\left(a\right)=6a-6>0;\forall a\in\left[2;3\right]\)
\(\Rightarrow f\left(a\right)\) đồng biến trên \(\left[2;3\right]\Rightarrow k_{max}\) khi \(a=3\)
\(\Rightarrow b=a^3-3a^2-1=-1\)
\(S=3-1=2\)

Hệ số góc của tiếp tuyến với \(\left( C \right)\) tại điểm \(A\) là:
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{\left( { - 2{{\rm{x}}^2}} \right) - \left( { - {{2.1}^2}} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 2{{\rm{x}}^2} + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 2\left( {{{\rm{x}}^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 2\left( {{\rm{x}} - 1} \right)\left( {{\rm{x}} + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \left[ { - 2\left( {{\rm{x}} + 1} \right)} \right] = - 2\left( {1 + 1} \right) = - 4\end{array}\)

Ý tưởng thế này: tọa độ A, B thỏa mãn:
\(\left\{{}\begin{matrix}6x^2+6ax=6\\y=2x^3+3ax^2+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2=1-ax\\y=2x^3+3ax^2+b\end{matrix}\right.\)
\(\Rightarrow y=2x\left(1-ax\right)+3a\left(1-ax\right)+b\)
\(\Rightarrow y=-2ax^2+2x-3a^2x+3a+b\)
\(\Rightarrow y=-2a\left(1-ax\right)+2x-3a^2x+3a+b\)
\(\Rightarrow y=\left(2-a^2\right)x+a+b\)
\(\Rightarrow\left(2-a^2\right)x-y+a+b=0\)
Đây chính là pt AB theo a;b
Từ khoảng cách \(\Rightarrow\dfrac{\left|a+b\right|}{\sqrt{\left(2-a^2\right)^2+1}}=1\Leftrightarrow\left(a+b\right)^2=\left(2-a^2\right)^2+1\)
\(\Leftrightarrow\left(a+b\right)^2=a^4-4a^2+5\)
\(\Leftrightarrow2a^2+\left(a+b\right)^2=a^4-2a^2+5=\left(a^2-1\right)^2+4\ge4\)

\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến d qua A có dạng: \(y=k\left(x-m\right)+1\)
d là tiếp tuyến của (C) khi hệ sau có nghiệm: \(\left\{{}\begin{matrix}\dfrac{2-x}{x-1}=k\left(x-m\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{2-x}{x-1}=\dfrac{m-x}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow-x^2+3x-2=m+x^2-3x+1\)
\(\Leftrightarrow-2x^2+6x-3=m\) (1)
Để từ A kẻ được đúng 1 tiếp tuyến \(\Rightarrow\) (1) có đúng 1 nghiệm thỏa mãn \(x\ne1\)
TH1: (1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1 \(\Rightarrow m=1\)
TH2: đường thẳng \(y=m\) cắt \(y=-2x^2+6x-3\) tại đúng 1 điểm
\(\Rightarrow m=\dfrac{3}{2}\)