Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện: \(x\ne1\)
a) Xét phương trình: \(\frac{x^2-2mx+3m-2}{x-1}=0\Leftrightarrow x^2-2mx+3m-2=0\)\(\left(x-1\ne0\right)\)
Pt có hai nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow m^2-3m+2>0\Leftrightarrow\orbr{\begin{cases}m>2\\m< 1\end{cases}}\)
Khi đó \(\hept{\begin{cases}x_1=m-\sqrt{m^2-3m+2}\\x_2=m+\sqrt{m^2-3m+2}\end{cases}}\)
+) \(x_1,x_2\ne1\Leftrightarrow\hept{\begin{cases}m-\sqrt{m^2-3m+2}\ne1\\m+\sqrt{m^2-3m+2}\ne1\end{cases}\Leftrightarrow m\ne1}\)
+) Tiếp tuyến của đồ thị tại hai giao điểm với trục Ox vuông góc với nhau
\(\Leftrightarrow\hept{\begin{cases}y'\left(x_1\right)=-1\left(1\right)\\y'\left(x_2\right)=1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow\frac{\left(2x_1-2m\right)\left(x_1-1\right)-\left(x_1^2-2mx_1+3m-2\right)}{\left(x_1-1\right)^2}=-1\)
\(\Leftrightarrow\frac{m-1}{\left(x_1-1\right)^2}=2\Rightarrow m-1=2\left(m-\sqrt{m^2-3m+2}-1\right)^2\)
\(\Leftrightarrow\left(m-1\right)\left[1-2\left(2m-3-2\sqrt{m^2-3m+2}\right)\right]=0\)
\(\Leftrightarrow4\sqrt{m^2-3m+2}=4m-7\Leftrightarrow\hept{\begin{cases}m\ge\frac{7}{4}\\m=\frac{17}{8}\end{cases}}\Leftrightarrow m=\frac{17}{8}\)(t/m m>2 v m<1)
Giải (2) cho ra \(m=1\)(loại). Vậy m cần tìm là \(m=\frac{17}{8}.\)

Bài 5. Cosx = ![]() là phương trình xác định hoành độ giao điểm của đường thẳng y =
là phương trình xác định hoành độ giao điểm của đường thẳng y = ![]() và đồ thị y = cosx.
và đồ thị y = cosx.
Từ đồ thị đã biết của hàm số y = cosx, ta suy ra x = ![]() , (k ∈ Z), ( chú ý tìm giao điểm của đường thẳng cới đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với
, (k ∈ Z), ( chú ý tìm giao điểm của đường thẳng cới đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với ![]() rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x là x =
rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x là x = ![]() , (k ∈ Z)).
, (k ∈ Z)).

\(y'=\dfrac{3}{\left(x+1\right)^2}\Rightarrow\) phương trình tiếp tuyến tại \(M\left(m;\dfrac{m-2}{m+1}\right)\) có dạng:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{m-2}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+m^2-4m-2=0\)
\(P=d\left(I;d\right)=\dfrac{\left|6m+6\right|}{\sqrt{9+\left(m+1\right)^4}}=\dfrac{6}{\sqrt{\left(m+1\right)^2+\dfrac{9}{\left(m+1\right)^2}}}\le\dfrac{6}{\sqrt{2\sqrt{\dfrac{9\left(m+1\right)^2}{\left(m+1\right)^2}}}}=\sqrt{6}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(m+1\right)^2=\dfrac{9}{\left(m+1\right)^2}\Leftrightarrow\left(m+1\right)^2=3\Rightarrow m=\) ... lại xấu :)

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
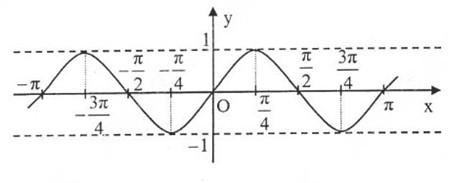
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)

\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1

Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)
\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến d qua A có dạng: \(y=k\left(x-m\right)+1\)
d là tiếp tuyến của (C) khi hệ sau có nghiệm: \(\left\{{}\begin{matrix}\dfrac{2-x}{x-1}=k\left(x-m\right)+1\\\dfrac{-1}{\left(x-1\right)^2}=k\end{matrix}\right.\)
\(\Rightarrow\dfrac{2-x}{x-1}=\dfrac{m-x}{\left(x-1\right)^2}+1\)
\(\Leftrightarrow-x^2+3x-2=m+x^2-3x+1\)
\(\Leftrightarrow-2x^2+6x-3=m\) (1)
Để từ A kẻ được đúng 1 tiếp tuyến \(\Rightarrow\) (1) có đúng 1 nghiệm thỏa mãn \(x\ne1\)
TH1: (1) có 1 nghiệm bằng 1 và 1 nghiệm khác 1 \(\Rightarrow m=1\)
TH2: đường thẳng \(y=m\) cắt \(y=-2x^2+6x-3\) tại đúng 1 điểm
\(\Rightarrow m=\dfrac{3}{2}\)