Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo

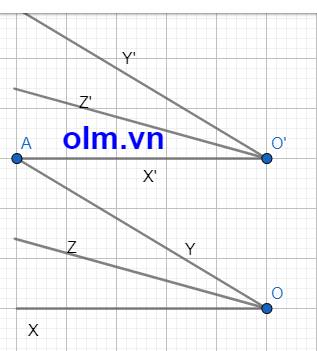
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
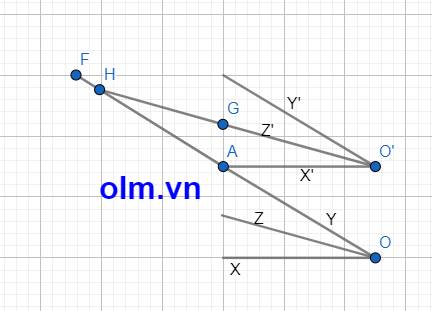
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)

Xét ΔOMA và ΔONA có
OM=ON
\(\widehat{MOA}=\widehat{NOA}\)
OA chung
Do đó: ΔOMA=ΔONA
Suy ra: \(\widehat{MAO}=\widehat{NAO}\)
hay AO là tia phân giác của góc MAN

a) Ta có: \(\widehat{xOy}=140^0\)
\(\widehat{xOA}=\widehat{yOB}=90^0\) ( do \(OA\perp Ox,OB\perp Oy\) )
\(\Rightarrow\widehat{AOB}=360-\left(\widehat{xOy}+\widehat{xOA}+\widehat{yOB}\right)\)
\(\Leftrightarrow\widehat{AOB}=360^0-\left(140^0+90^0+90^0\right)\)
\(\Leftrightarrow\widehat{AOB}=40^0\)
\(OM\) là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOM}=\widehat{MOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.140^0=70^0\)
\(OM'\) là tia đối của \(OM\Rightarrow\widehat{MOM'}=180^0\)
Mà \(OA\) nằm ngoài \(\widehat{xOy}\) và \(OA\perp Ox\) nên \(\widehat{MOM'}=\widehat{MOx}+\widehat{xOA}+\widehat{AOM'}\)
Do đó \(\widehat{AOM'}=\widehat{MOM'}-\left(\widehat{MOx}+\widehat{xOA}\right)\) \(\Rightarrow\widehat{AOM'}=180^0-\left(70^0+90^0\right)=20^0\) \(\left(1\right)\)
Mặt khác \(Oy\) nằm giữa \(OB\) và \(OM\) nên \(\widehat{MOB}=\widehat{MOy}+\widehat{yOB}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOB}< \widehat{MOM'}\)
Do đó \(OB\) và \(Oy\) nằm cùng nửa mặt phẳng bờ \(MM'\)
\(Ox\) nằm giữa \(OA\) và \(OM\) nên\(\widehat{MOA}=\widehat{MOx}+\widehat{xOA}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOA}< \widehat{MOM'}\)
Do đó tia \(OA\) và \(Ox\) nằm cùng nửa mặt phẳng bờ \(MM'\)
Nên \(OM'\) nằm giữa \(OA\) và \(OB\)
\(\Rightarrow\widehat{AOB}=\widehat{AOM'}+\widehat{M'OB}\Rightarrow\widehat{M'OB}=\widehat{AOB}-\widehat{AOM'}=40^0-20^0=20^0\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{M'OB}=\widehat{AOM'}=20^0=\dfrac{1}{2}\widehat{AOB}\)
Suy ra \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
b) Ta có: \(\widehat{MOx}< \widehat{MOA}< \widehat{MOM'}\) nên \(OA\) nằm giữa \(Ox\) và \(OM'\)
Mà \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
Suy ra \(OA\) nằm giữa \(Ox\) và \(OB\)
Vậy \(\widehat{xOB}=\widehat{xOA}+\widehat{AOB}=90^0+40^0=130^0\)

a. Ta có: O m ⊥ Ox
⇒ x O m ^ = 90 0 < x O y ^
Ta có Om nằm trong x O y ^ nên:
Tương tự ta có: x O n ^ = x O y ^ − 90 0
Do đó: x O n ^ = y O m ^ = x O y ^ − 90 0 (1)
b. Gọi Ot là tia phân giác của m O n ^ ⇒ n O t ^ = m O t ^ (2)
Theo đề bài, ta có : m O n ^ nằm trong x O y ^
Mà Ot là tia phân giác của m O n ^
⇒ Tia Ot nằm giữa hai tia Ox và Oy Tia On nằm giữa hai tia Ox và Ot Tia Om nằm giữa hai tia Oy và Ot
⇒ x O t ^ = x O n ^ + n O t ^ , y O t ^ = y O m ^ + m O t ^ (3)
Từ (1), (2), (3) suy ra: x O t ^ = y O t ^
Ta có tia Ot nằm giữa hai tian Ox và Oy; x O t ^ = y O t ^
=> Ot là tia phân giác của x O y ^
Do đó Ot là tia phân giác chung của m O n ^ và x O y ^