Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

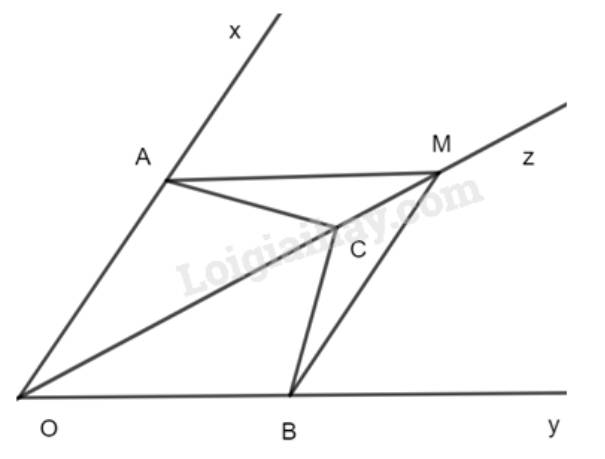
a) Trong \(\Delta OAC\) có: \(\widehat {AOC}+\widehat {OAC}+\widehat {OCA}=180^0\)
Trong \(\Delta OBC\) có: \(\widehat {BOC}+\widehat {OBC}+\widehat {OCB}=180^0\)
Mà \(\widehat {AOC} = \widehat {BOC}\)(do Oz là phân giác góc xOy) và \(\widehat {CAO}=\widehat {CBO}\)
Do đó, \(\widehat {OCA}=\widehat {OCB}\).
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(\widehat {AOC} = \widehat {BOC}\) (cmt)
OC chung
\(\widehat {OCA} = \widehat {OCB}(cmt)\)
\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)
b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)
Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù
\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù
Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)
Xét \(\Delta MAC\) và \(\Delta MBC\) có:
AC=BC (cmt)
\(\widehat {ACM} = \widehat {BCM}\) (cmt)
CM chung
\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)

`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`

Xét \(\Delta\)AOM và \(\Delta\)BOM có:
OA=OB (gt)
góc AOM=góc BOM (do Oz là phân giác góc xOy)
OM chung
=> \(\Delta\)AOM = \(\Delta\)BOM (c.g.c) (1)
(1) => góc AMO=góc BMO (2 góc tương ứng)
=> MO là phân giác góc AMB (dpcm)
(1) => AM=BM (2 góc tương ứng)
=> \(\Delta\)ABM cân tại M (dhnb)
Xét \(\Delta\)ABM cân tại M có tia phân giác MO đồng thời là đường trung trực của cạnh AB (t/c các đường đặc biệt trong \(\Delta\)cân) (dpcm)

a, Vì Oz là tia phân giác của xOy
=> xOz = zOy = xOy/2 = 60o/2 = 30o
b, Xét △OIA và △ OIB
Có: OA = OB
AOI = IOB
OT là cạnh chung
=> △OIA = △OIB (c.g.c)
c, Vì △OIA = △OIB
=> AIO = OIB (2 góc tương ứng)
Mà AIO + OIB = 180o (2 góc kề bù)
=> AIO = OIB = 90o
=> OI vuông góc AB
Hình dễ tự vẽ
a ) Oz là tia p/g của góc xOy => \(\widehat{xOz}=\widehat{zOy}=\frac{1}{2}.\widehat{xOy}=30^o\)
=> góc zOy = 30 độ
b ) Xét tam giác OIA và tam giác OIB có :
OA = OB ( gt )
\(\widehat{xOz}=\widehat{zOy}\)( Oz là tia p/g của góc xOy )
OI là cạnh chung
=> Tam giác OIA = Tam giác OIB ( c.g.c )
b ) Do tam giác OIA = tam giác OIB ( cm trên ) => \(\widehat{OIA}=\widehat{OIB}\)
Ta có :
\(\widehat{OIA}+\widehat{OIB}=180^o\)( hai góc kề bù )
\(\widehat{OIA}+\widehat{OIA}=180^o\)
\(\widehat{OIA}.2=180^o\)
=> \(\widehat{OIA}=90^o\)
=> OI vuông góc với AB

a) ta có \(OP+PQ=OQ\)
\(OM+MN=ON\)
mà \(OP=OM;PQ=MN\)
\(\Rightarrow OQ=ON\)
Xét \(\Delta NOPvà\Delta QOMcó\)
\(OP=OM\) ( giả thiết )
\(\widehat{QON}\) là góc chung
\(OQ=ON\) (chứng minh trên)
\(\Rightarrow\Delta NOP=\Delta QOM\left(c-g-c\right)\)
vậy \(\Delta NOP=\Delta QOM\)
b) tự làm nhé
Xét ΔOMA và ΔONA có
OM=ON
\(\widehat{MOA}=\widehat{NOA}\)
OA chung
Do đó: ΔOMA=ΔONA
Suy ra: \(\widehat{MAO}=\widehat{NAO}\)
hay AO là tia phân giác của góc MAN