Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Gọi P là trung điểm của AC.
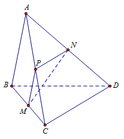
Ta có: P N / / C D , M P / / A B ⇒ A B ; C D = M P ; P N
P N = M P = a 2 , M N = a 3 2 ⇒ cos M P N ⏜ = − 1 2 ⇒ M P N ⏜ = 120 °
⇒ A B ; C D ⏜ = 60 °
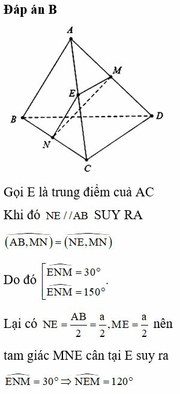
Đáp án B
Gọi E là trung điểm AC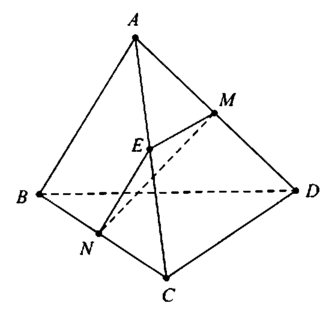
Khi đó NE//AB suy ra A B ; M N ^ = N E ; M N ^
Do đó [ E N M ^ = 30 ° E N M ^ = 150 °
Lại có N E = A B 2 = a 2 ; M E = a 2 nên tam giác MNE cân tại E suy ra E N M ^ = 30 ° ⇒ N E M ^ = 120 °
Suy ra M N = M E 2 + N E 2 - 2 M E . N E . cos N E M ^ = a 3 2 .
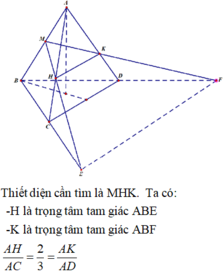
Đáp án D
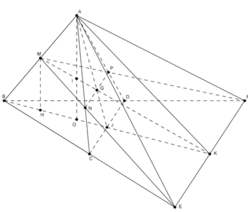
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
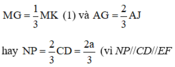
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là
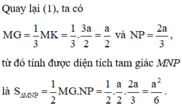
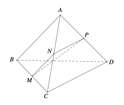
Đáp án A
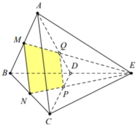
Nối 
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích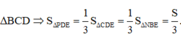 
Họi h là chiều cao của tứ diện ABCD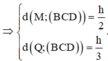 
Khi đó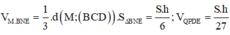 
Suy ra
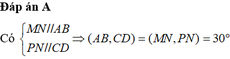
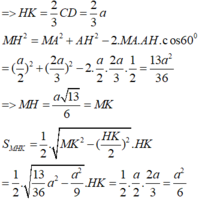
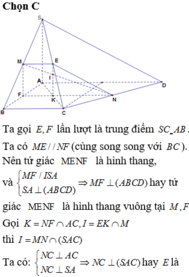
Đáp án C
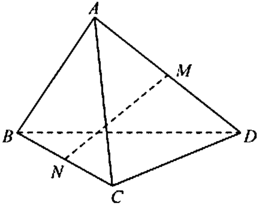
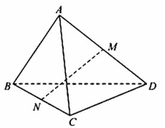
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó ( A B , C D ^ ) = ( M P , M Q ^ ) = P M Q ^
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được M P = M Q = N P = N Q = a hay tứ giác MPNQ là hình thoi.