Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án D
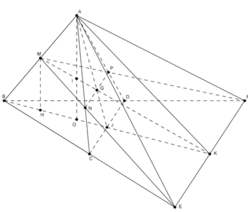

Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
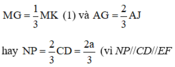
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là


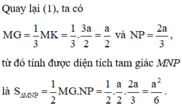

Bài giải
Ta có sơ đồ :
CDHHCN : I-----I-----I-----I-24,2-I
CRHHCN : I-----I-----I-----I
Hiệu số phần bằng nhau là :
5 - 3 = 2 ( phần )
Chiều rộng là : ( 24,2 : 2 ) x 3 = 36,3 ( cm )
Chiều dài là : 36,3 + 24,2 = 60,5 ( cm )
Chiều cao là : 36,3 : 2 = 18,15 ( cm )
Diện tích xung quanh là : ( 36,3 + 60,5 ) x 2 x 18,15 = 3513,84 ( cm2)
Diện tích toàn phần là : 3513,84 + 36,3 x 30,25 x 2 = 214783,47 ( cm2)
Thể tích là : 36,3 x 60,5 x 18,15 = 39860,1225 (cm3)
DS :...
Ta có sơ đồ :
CDHHCN : I-----I-----I-----I-24,2-I
CRHHCN : I-----I-----I-----I
Hiệu số phần bằng nhau là :
5 - 3 = 2 ( phần )
Chiều rộng là : ( 24,2 : 2 ) x 3 = 36,3 ( cm )
Chiều dài là : 36,3 + 24,2 = 60,5 ( cm )
Chiều cao là : 36,3 : 2 = 18,15 ( cm )
Diện tích xung quanh là : ( 36,3 + 60,5 ) x 2 x 18,15 = 3513,84 ( cm2)
Diện tích toàn phần là : 3513,84 + 36,3 x 30,25 x 2 = 214783,47 ( cm2)
Thể tích là : 36,3 x 60,5 x 18,15 = 39860,1225 (cm3)
DS :...

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Bài 1 :Diện tích hình tròn bằng bình phương bán kính nhân với Pi. Như vậy, nếu đường kình giảm 50% thì bán kính giảm 50%. Khi đó diện tích sẽ bằng: 50% bán kính( nhân) 50% bán kính (nhân) Pi= 25% bán kính nhân Pi= 25% diện tích hình tròn ban đầu. Như vậy diện tích hình tròn giảm đi: 100%-25%= 75%
Bài 2 : Diện tích hình tròn = Số Pi x R^2
1. Lúc chưa tăng bán kính lên 10% thì:
S(1) = Pi x R^2
2. Khi tăng bán kính lên 10% thì:
S(2) = Pi x (110%. R)^2
S(2) = Pi x (1,1.R)^2
S(2) = Pi x 1,21.R^2
3. Diện tích hình tròn tăng lên là:
S(2) - S(1)
= (Pi x 1,21.R^2) - (Pi x R^2)
= (1,21 x Pi x R^2) - (1 x Pi x R^2)
= (Pi x R^2) x (1,21 - 1)
= 0,21 x Pi x R^2
Mà:
S(1) = Pi x R^2
Nên diện tích tăng lên là: 0,21 x S(1)
Hay nói cách khác là tăng lên 21%
Đáp số: 21%

Cạnh hình vuông là một số nguyên, do đó diện tích của hình vuông chính là số chính phương ( vì diện tích hình vuông là bình phương của cạnh hình vuông).
Thấy: diện tích hình vuông là 1 số gồm 2001 chữ số 1, có tổng các chữ số là:
1.2001=20011.2001=2001
2001 là 1 số chia hết cho 3, vì vậy mỗi cạnh hình vuông đều phải chia hết cho 3, đặt cạnh hình vuông là 3k (k∈Z)
Diện tích là (3k)2=9k2
Như vậy diện tích là 1 số chia hết cho 9. Mà 2001 không chia hết cho 9
⇒Không tồn lại 1 hình vuông mà số đo độ dài các cạnh là số nguyên và số đo diện tích là 1111.....111 (2001 chữ số 1)
Vậy không tồn lại 1 hình vuông mà số đo độ dài các cạnh là số nguyên và số đo diện tích là 1111.....111 (2001 chữ số 1)


Đáp án là D