L
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
2
AH
Akai Haruma
Giáo viên
6 tháng 1
Lời giải:
Không mất tổng quát giả sử $a\leq b\leq c$
Nếu $a,b,c$ đều là số nguyên tố lẻ thì $a^2+b^2+c^2$ là số lẻ. Mà $5070$ chẵn nên vô lý.
Do đó trong 3 số $a,b,c$ tồn tại ít nhất 1 số chẵn.
Số nguyên tố chẵn luôn là số bé nhất (2) nên $a=2$
Khi đó: $b^2+c^2=5070-a^2=5066\geq 2b^2$
$\Rightarrow b^2\leq 2533$
$\Rightarrow b< 51$
$\Rightarrow b\in \left\{2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47\right\}$
Thử các TH này ta thấy $(b,c)=(5,71), (29,65)$
Vậy $(a,b,c)=(2,5,71), (2,29,65)$ và các hoán vị.
12 tháng 4
vì 5070 là số chẵn ⇒ một trong 3 số a,b,c chẵn hoặc cả 3 số a,b,c chẵn
+) cả 3 số a,b,c chẵn
=> a=2, b=2, c=2 ( vì a,b,c là các số nguyên tố )
khi đó: a2+b2+c2= 12(loại)
=> một trong 3 số a,b,c chẵn
vì giá trị các số bằng nhau, giả sử a chẵn => a=2
khi đó: a2+b2+c2= 4+b2+c2
=> b2+c2= 5066
vì số chính phương có tận cùng là 0, 1, 4, 5, 6, 9 mà b2 và c2 là số chính phương có tận cùng là 0, 1, 4, 5, 6, 9
=> b2 và c2 có tận cùng là 0, 1, 4, 5, 6, 9
Mà b và c lẻ
=> b2 và c2 có tận cùng là 1, 5, 9
mà 5066 có tận cùng là 6
=> b2 và c2 có tận cùng là 1, 5
=> b và c có tận cùng là 1, 5
giả sử b có tận cùng là 5=> b=5
khi đó: 25+ c2 = 5066
c2 = 5041=712
=> c = 71
vậy, a=2, b=5, c=71 và các hoán vị của nó
VN
1
3 tháng 7 2023
a^3+b^3+c^3-3abc
=(a+b)^3+c^3-3ab(a+b)-3bca
=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2023
Nếu a;b;c cùng lẻ \(\Rightarrow a^2+b^2+c^2\) lẻ, mà 1386 chẵn nên ko thỏa mãn
\(\Rightarrow\) Trong 3 số a;b;c phải có ít nhất 1 số chẵn, không mất tính tổng quát, giả sử c chẵn. Mà c là số nguyên tố \(\Rightarrow c=2\)
\(\Rightarrow a^2+b^2+4=1398\Rightarrow a^2+b^2=1394\)
Mặt khác một số chính phương chia 5 chỉ có các số dư 0,1,4
Mà \(1394\) chia 5 dư 4 \(\Rightarrow a^2+b^2\) chia 5 dư 4
\(\Rightarrow\) Trong 2 số \(a^2\) và \(b^2\) một số chia 5 dư 0, một số chia 5 dư 4
Hay trong 2 số a và b phải có 1 số chia hết cho 5
Giả sử b chia hết cho 5 \(\Rightarrow b=5\)
\(\Rightarrow a^2+25=1394\Rightarrow a=37\)
Vậy \(\left(a;b;c\right)=\left(37;5;2\right);\left(37;2;5\right);\left(2;5;37\right);\left(2;37;5\right);\left(5;2;37\right);\left(5;37;2\right)\)
17 tháng 2 2021
a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb
MH
15 tháng 1 2016
4. a. A = -a + b - c + a + b + c = 2b
b. Thay b = -1 vào A => A = 2.(-1) = -2
5. a. = (1-2) + (3-4) + (5-6) + ... + (99-100) (có tất cả 50 cặp)
= -1 + (-1) + ... + (-1)
= -1.50
= -50
b. = (4-2) + (8-6) + ... + (2016 - 2014) ( có tất cả 504 cặp )
= 2 + 2 + ... + 2
= 2.504
= 1008
15 tháng 1 2016
4) a) A=(-a+b-c)-(-a-b-c)=-a+b-c+a+b+c=(-a+a)+(b+b)+(-c+c)=0+2b+0=2b
5)a) -50
b) 1008
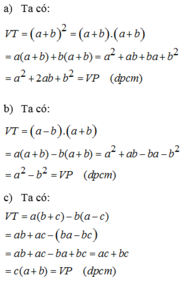
ta là dương Minh Đức lớp 6a5 trường htk at cần thơ
=1 bạn nhân cái đã cho với a+b+c ,sau đó tách thôi,,,VD a(a+b+c)/(b+c)=a+1 ( tách ra nha) tương tự vs mấy cái kai