Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
có 18 số cần tìm.
gọi số cần tìm là abc
xét a=1, c có 3 cách chọn(0,2,8), b có 4 cách => có 3*4=12
xét abc<270, a=2, nếu c=8 thì b có 3 cách, nếu c=0 thì b có 2 cách => có 1*1*3+1*1*2=6
xét 270 đến 278, ko có số thảo mãn
Số có 4 chữ số có dạng 
Số phần tử của không gian mẫu: n(S)=9.9.8.7=4536.
Gọi A: “ tập hợp các số tự nhiên có 4 chữ số phân biệt và lớn hơn 2500.”
TH1: a>2
Chọn a: có 7 cách chọn.
Chọn b: có 9 cách chọn.
Chọn c: có 8 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có:7.9.8.7=3528 .
TH2: a=3; b>5
Chọn a: có 1 cách chọn.
Chọn b: có 4 cách chọn.
Chọn c: có 8cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.4.8.7=224 (số).
TH3: a=2; b=5; c>0
Chọn a: có 1 cách chọn.
Chọn b: có1 cách chọn.
Chọn c: có 7 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.7.7=49(số).
TH4. a=2; b=5; c=0 ;d>0
Chọn a: có 1 cách chọn.
Chọn b: có 1 cách chọn.
Chọn c: có 1 cách chọn.
Chọn d: có 7 cách chọn.
Vậy trường hợp này có: 1.1.1.7=7(số).
Như vậy: n(A)=3528+224+49+7=3808
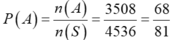
Chọn C.
Xét số 
được lập từ các chữ số thuộc tập A.
Vì x lẻ nên e ∈ {1; 3; 5; 7} , suy ra có 4 cách chọn e. Bốn chữ số còn lại được chọn từ 7 chữ số của tập A \ {e} nên có cách
Suy ra, có 4.840=3360 số lẻ gồm năm chữ số khác nhau.
Mà số x bắt đầu bằng 123 có số.
Vậy số x thỏa yêu cầu bài toán là :3360- 20=3340 số.
Chọn A.
gọi 3 chữ số có dang abc
chọn a có 6c
chọn b \ a có 5c
chọn c \a\b có 4 c
=> có 120 c
Xét tập B={ 1;4;5;6;7;8}, ta có B không chứa số 3.
X là một tập con của A thỏa yêu cầu bài toán khi và chỉ khi X \ {2} là một tập con của B . Do đo, số tập con của A thỏa yêu cầu bài toán bằng số tập con của B và bằng 26 = 64
Chọn A.
