Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác FNIM có
\(\widehat{FNI}+\widehat{FMI}=180^0\)
nên FNIM là tứ giác nội tiếp
hay F,N,I,M cùng thuộc 1 đường tròn
b: Xét tứ giác DNME có
\(\widehat{DNE}=\widehat{DME}\left(=90^0\right)\)
nên DNME là tứ giác nội tiếp
hay D,N,M,E cùng thuộc 1 đường tròn

a: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=180^0\)
nên AEHD là tứ giác nội tiếp
hay A,E,H,D cùng thuộc 1 đường tròn
b: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}\)
nên BEDC là tứ giác nội tiếp
hay B,E,D,C cùng thuộc 1 đường tròn

a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}\left(=90^0\right)\)
Do đó: ENMF là tứ giác nội tiếp
b: Xét tứ giác DNIM có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DNIM là tứ giác nội tiếp
a, Xét ΔENF vuông tại N
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
Xét ΔEMF vuông tại M
⇒ EF là đường kính của đường tròn có tâm là trung điểm của EF
⇒ M,N,E,F cùng thuộc 1 đường tròn đường kính EF
b,Tương tự

a: Xét tứ giác ENMF có
\(\widehat{ENF}=\widehat{EMF}=90^0\)
Do đó: ENMF là tứ giác nội tiếp
hay E,N,M,F cùng thuộc 1 đường tròn
b: Xét tứ giác DMIN có
\(\widehat{DNI}+\widehat{DMI}=180^0\)
Do đó: DMIN là tứ giác nội tiếp
hay D,M,I,N cùng thuộc 1 đường tròn

a, ta có BM , CN là các đường cao \(=>\angle\left(BMC\right)=\angle\left(CNB\right)=90^o\)(1)
mà N,M là 2 đỉnh liên tiếp của tứ giác BNMC
\(=>\) tứ giác BMNC nội tiếp đường tròn
=>4 điểm B,M,N,C cùng thuộc 1 đường tròn
b, có AD là đường kính (O) =>tam giác ACD nội tiếp (O)
\(=>\angle\left(ACD\right)=90^o\)(2)
từ(1)(2) \(=>BM//CD=>BH//CD\left(3\right)\)
tương tự =>tam giác ABD nội tiếp (O)\(=>\angle\left(ABD\right)=90^o\left(4\right)\)
từ(1)(4) \(=>BD//CN< =>CH//BD\left(5\right)\)
từ(3)(5)=>BHCD là hình bình hành

Lời giải:
1.
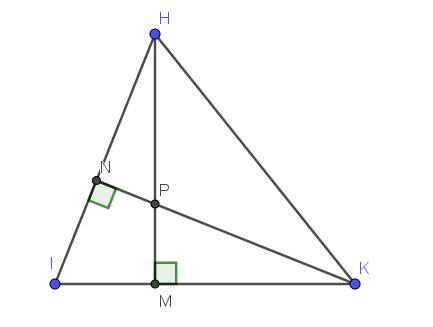
Xét tứ giác $HNMK$ có $\widehat{HNK}=\widehat{HMK}=90^0$. Mà 2 góc này cùng nhìn cạnh $HK$ nên $HNMK$ là tứ giác nội tiếp.
$\Rightarrow H,N,M,K$ cùng thuộc 1 đường tròn.
2.
Xét tứ giác $INPM$ có tổng 2 góc đối nhau $\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0$ nên $INPM$ là tứ giác nội tiếp.
$\Rightarrow I,N, P,M$ cùng thuộc 1 đường tròn.

1: Xét tứ giác HNMK có
\(\widehat{HNK}=\widehat{HMK}=90^0\)
=>HNMK là tứ giác nội tiếp đường tròn đường kính HK
=>H,N,M,K cùng thuộc 1 đường tròn
2: Xét tứ giác INPM có
\(\widehat{INP}+\widehat{IMP}=90^0+90^0=180^0\)
=>INPM là tứ giác nội tiếp
=>I,N,P,M cùng thuộc 1 đường tròn

a: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
nên ADHE là tứ giác nội tiếp
hay A,D,H,E cùng thuộc một đường tròn

a: Xét tứ giác ADHE có
\(\widehat{ADH}+\widehat{AEH}=180^0\)
Do đó: ADHE là tứ giác nội tiếp
hay A,D,H,E cùng thuộc 1 đường tròn

Xét \(\left(\dfrac{EK}{2}\right)\) có
ΔKME nội tiếp đường tròn
KE là đường kính
Do đó: ΔKME vuông tại M
Xét \(\left(\dfrac{FK}{2}\right)\) có
ΔFNK nội tiếp đường tròn
FK là đường kính
Do đó: ΔFNK vuông tại N
Xét tứ giác DMKN có \(\widehat{DMK}=\widehat{DNK}=\widehat{MDN}=90^0\)
nên DMKN là hình chữ nhật
hay D,M,K,N cùng thuộc 1 đường tròn
a, có DM _|_ EF và EN _|_ DF (gt)
=> ^IMF = ^INF = 90
=> M;N thuộc đường tròn đường kính IF (Định lí)
=> F;N;I;M thuộc đường tròn đk IF
b, có DM _|_ EF và EN _|_ DF (gt)
=> ^END = ^DME = 90
=> N;M thuộc đường tròn đk DE
=> D;N;M;E cùng thuộc đường tròn đk DE