Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy F là trung điểm BC
EF//AD và AE//DF => ADFE là hình bình hành => tam giác ADE = tam giác EDF
ED//CF và EC//DF => EDFC là hình bình hành => tam giác EDF = tam giác EFC
ED//FB và EF//DB => EDBF là hình bình hành => tam giác EDF = tam giác DBF
Diện tích tam giác ABC :
S(ABC) = S(ADE) x 4 = 60 x 4 = 240 cm2

vì D và E là trung điểm của AB và AC => tam giác ADE = 1/2 ABC
=> ADE= 360 / 2 =180 ( cm2)
đ/s:....
tk choi mình nha!!!
Stam giác ABC = \(\frac{AB.AC}{2}=360cm^2\)
Vì D là trung điểm của AB
=> AD = DB
Vì E là trung điểm của AC
=> AE = EC
Stam giác ADE = \(\frac{\frac{AB}{2}.\frac{AC}{2}}{2}=\frac{AB.AC.\frac{1}{4}}{2}=\frac{AB.AC}{8}=\frac{360}{8}=45cm^2\)

Cho tam giác ABC có diện tích 360 cm2. Lấy D và E là trung điểm các cạnh AB và AC. Nối D với E. Tính diện tích tam giác ADE.
Kết quả: 90 cm2
Xem cách giải chi tiết tại: https://olm.vn/hoi-dap/question/240248.html
K mk nha bn. Thanks

Nối E với B
Xét hai tam giác ABE và ABC
- Chùng chiều cao hạ từ đỉnh B xuống AC
- AE = 1/2AC
=> SABE = SABC x 1/2 = 360 x 1/2 = 180 ( cm2 )
Xét hai tam giác ADE và ABE
- Chung chiều cao hạ từ đỉnh E xuống AB
- AD = 1/2 AB
=> SADE = SABE x 1/2 = 180 x 1/2 = 90 ( cm2 )
Đáp số : 90 cm2

Xét tam giác CAD và CAB có
+ Chung đường cao hạ từ đỉnh C
+ Đáy AD =\(\frac{1}{2}\) AB
\(\Rightarrow\) S cad = \(\frac{1}{2}\) S cab = 360. \(\frac{1}{2}\) = 180(cm2)
Xét tam giác DAE và DAC có:
+ Chung đường cao hạ từ đỉnh D
+ Đáy AE = \(\frac{1}{2}\) AC
\(\Rightarrow\) S dae = \(\frac{1}{2}\) S dac = 180.\(\frac{1}{2}\) =90(cm2)
Đáp số : 90 cm2
Nhìn vào hình vẽ ta có dt tg ADE = dt tg BDE ½ dttg ABE ABC ( Vì có chung chiều cao hạ từ đỉnh E và có cạnh đáy AD = DB)
Và dt tg ABE = dttg BEC = ½ dttg ABC ( Vì có chung chiều cao hạ từ đỉnh B và có cạnh đáy AE = EC). Vậy Diện tích tam giác ADE = ¼ Diện tích tam giác ABC. Diện tích tam giác ADE là : 360: 4 = 90 .

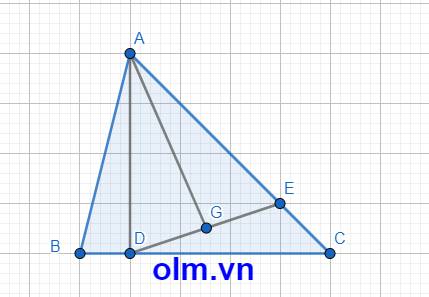
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%