Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABCD có
N là trung điểm của AC
N là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN=1/2BC

Tham khảo
a) Xét ΔAMH và ΔNMB có:
+ AM = NM
+ góc AMH = góc NMB (đối đỉnh)
+ MH = MB
=> ΔAMH = ΔNMB (c-g-c)
=> góc MAH = góc MNB
=> AH//BN
Mà AH vuông góc BC
=> BN vuông góc BC
b) Do ΔAMH = ΔNMB
=> AH = BN
Trong tam giác vuông ABH vuông tại H
=> AB > AH (cạnh huyền là cạnh lớn nhất)
=> AB > BN
c) Ta cm được ΔABM = ΔNHM (c-g-c)
=> góc BAM = góc HNM
Trong ΔANH có:NH > AH
=> góc MAH > góc MNH
=> góc MAH > góc BAM
d) Ta cm được ΔABH = ΔACH (ch-cgv)
=> BH = CH
=> CH = 2. HM
Tam giác ANC có CM là đường trung tuyến (do M là trung điểm của AN)
và CH/CM =2/3
=> H là trọng tâm của ΔANC
=> AH là đường trung tuyến
=>AH đi qua trung điểm của CN
hay A,H,I thẳng hàng
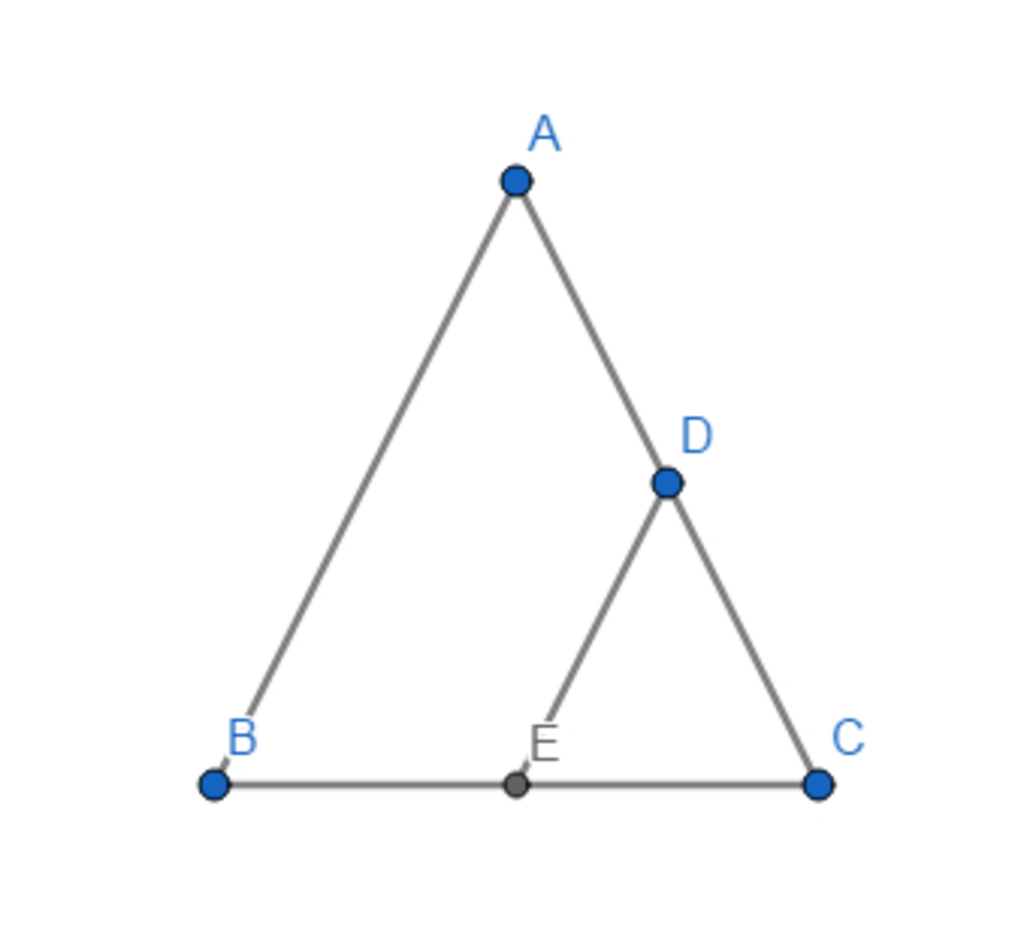

Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó: AMCD là hình bình hành
Suy ra: CD//AM
hay CD//AB

Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó: AMCD là hình bình hành
Suy ra: CD//AM
hay CD//AB

a) Ta có: B,A,D thẳng hàng(gt)
mà AB=AD(gt)
nên A là trung điểm của BD
Ta có: B,M,C thẳng hàng(gt)
mà BM=CM(gt)
nên M là trung điểm của BC
Ta có: D,N,C thẳng hàng(gt)
mà DN=NC(gt)
nên N là trung điểm của DC
Xét ΔDBC có
A là trung điểm của BD(cmt)
M là trung điểm của BC(cmt)
Do đó: AM là đường trung bình của ΔDBC(Định nghĩa đường trung bình của tam giác)
⇒AM//DC và \(AM=\dfrac{DC}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà N∈DC và \(CN=\dfrac{DC}{2}\)(N là trung điểm của DC)
nên AM//NC và AM=NC
Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇒AM⊥BC
⇒\(\widehat{AMC}=90^0\)
Xét tứ giác AMCN có
AM//CN(cmt)
AM=CN(cmt)
Do đó: AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AMCN có \(\widehat{AMC}=90^0\)(cmt)
nên AMCN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒\(\widehat{MAN}=90^0\)
hay AM⊥AN(đpcm)
b) Xét ΔDBC có
A là trung điểm của BD(cmt)
N là trung điểm của DC(cmt)
Do đó: AN là đường trung bình của ΔDBC(Định nghĩa đường trung bình của tam giác)
⇒AN//BC và \(AN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(đpcm)
c) Ta có: A là trung điểm của BD(cmt)
nên \(AB=\dfrac{BD}{2}\)
mà AB=AC(gt)
nên \(CA=\dfrac{BD}{2}\)
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(A là trung điểm của BD)
\(CA=\dfrac{BD}{2}\)(cmt)
Do đó: ΔBCD vuông tại C(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(\widehat{BCD}=90^0\)(đpcm)
Chứng minh:
Tam giác ABC có:
M là trung điểm của AB( theo giả thiết)
N là trung điểm của AC( theo giả thiết)
=>MN là đường trung bình của tam giác ABC
=> MN=1/2 BC
Chứng minh định lý:
Trên tia đối của tia NM lấy điểm D sao cho N là trung điểm của MD
Xét tam giác ANM và tam giác CND
Ta có:
AN=NC( theo giả thiết)
Góc ANM=gócCND( hai góc đối đỉnh)
NM=ND(cách vẽ)
Do đó:
Tam giác ANM = tam giác CND( c.g.c)
=> AM=CD( hai cạnh tương ứng)
Và góc A= góc MCD(hai góc tương ứng)
=> AM//CD
=> MB//CD
=> MBCD là hình thang
Lại có:
AM=CD
=> MD=BC và MD//BC
=> MN//BC
Mà N là trung điểm của MD(cách vẽ)
=> MN=1/2 MD
vẽ hình cho mk với