Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

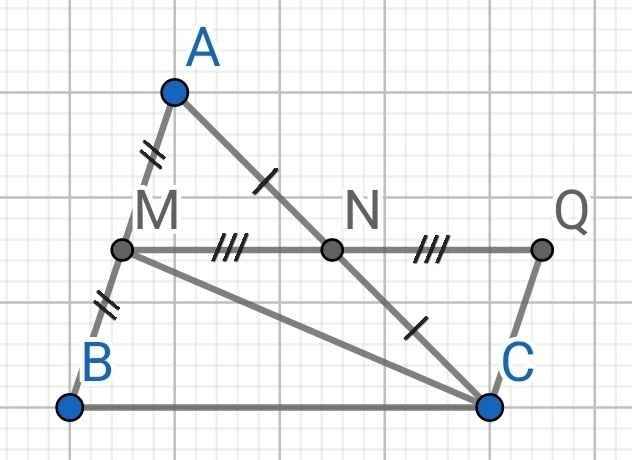
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC

tự kẻ hình nha
a) xét tam giác AMN và tam gáic CEN có
AN=NC(gt)
MN=NE(gt)
ANM=CNE( đối đỉnh)
=> tam giác AMN= tam giác CEN(cgc)
=> AM=CE(hai cạnh tương ứng) mà AM=MB=> MB=CE
=> CEN=AMN(hai góc tương ứng)
mà CEN so le trong với AMN mà A,M,B thẳng hàng=> MB//CE
c) từ MB//CE=> BMC=MCE( so le trong)
xét tam giác BMC và tam gíac ECM có
MC chung
BMC=MCE(cmt)
MB=CE(cmt)
=> tam gíac BMC= tam giác ECM(ccg)
d) từ tam giác BMC= tam giác CEM=> BCM=EMC( hai góc tương ứng), ME=BC( hai cạnh tương ứng)
mà BCM so le trong với EMC=> MN//BC
vì MN=NE mà ME=BC(cmt)
=> BC=2MN=> MN=1/2BC
Tu ve nhe
Xet tam giac AMN va tam giac CKN
MN=NK
Goc ANM=goc KNC ( doi dinh)
AN=NC
=>tam giacAMN=tam giac CKN
b, ta có goc AMN=goc NKC ( 2 canh tg ung)
Ta co hai goc nay o vi tri slt =>MB//KC
Ta co KC=AM( 2 canh tg ung)
AM=MB
=>MB=KC