Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}=90^0-\widehat{ACB}=90^0-30^0\)
hay \(\widehat{ABC}=60^0\)
Ta có: ΔAHB vuông tại A(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{BAH}=90^0-\widehat{ABH}=90^0-60^0=30^0\)
Ta có: tia AH nằm giữa hai tia AB,AC
nên \(\widehat{BAH}+\widehat{CAH}=\widehat{BAC}\)
hay \(30^0+\widehat{CAH}=90^0\)
\(\Leftrightarrow\widehat{CAH}=60^0\)
Ta có: AD là tia phân giác của \(\widehat{CAH}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{CAH}}{2}=\dfrac{60^0}{2}=30^0\)
Vậy: \(\widehat{ABC}=60^0\); \(\widehat{DAC}=30^0\)
b) Xét ΔADH và ΔADE có
AH=AE(gt)
\(\widehat{HAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{HAE}\))
AD chung
Do đó: ΔADH=ΔADE(c-g-c)
⇒\(\widehat{AHD}=\widehat{AED}\)(hai góc tương ứng)
mà \(\widehat{AHD}=90^0\)(AH⊥HD)
nên \(\widehat{AED}=90^0\)
hay DE⊥AC(đpcm)
c) Ta có: ΔAHD=ΔAED(cmt)
nên HD=ED(hai cạnh tương ứng)
Xét ΔFHD vuông tại H và ΔCED vuông tại E có
FH=CE(gt)
HD=ED(cmt)
Do đó: ΔFHD=ΔCED(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{FDH}=\widehat{CDE}\)(hai góc tương ứng)
mà \(\widehat{CDE}+\widehat{HDE}=180^0\)(hai góc kề bù)
nên \(\widehat{FDH}+\widehat{EDH}=180^0\)
⇒\(\widehat{FDE}=180^0\)
hay F,D,E thẳng hàng(đpcm)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
=>B nằm trên đường trung trực của AE(2)
Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm I của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC và AK=EC
Ta có: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của CK(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng
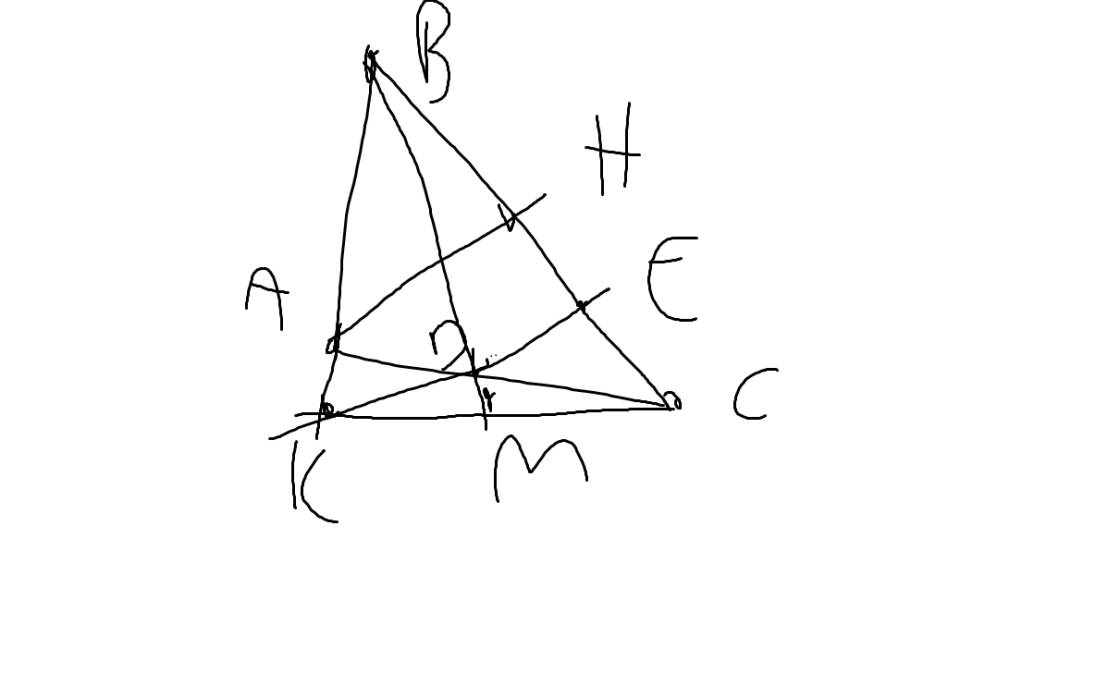

CM : a) Ta có: t/giác ABC cân tại A
=> góc B2 = góc C2
Mà góc B1 + góc B2 = 1800
góc C1 + góc C2 = 1800
=> góc B1 = góc C1
Xét t/giác AMB và t/giác ANC
có AB = AC (gt)
góc B1 = góc C1 (cmt)
MB = NC (gt)
=> t/giác AMB = t/giác ANC (c.g.c)
=> AM = AN (hai cạnh tương ứng)
=> t/giác AMN là t/giác cân tại A
b) Ta có: t/giác AMN cân tại A
=> góc M = góc N
Xét t/giác BME và t/giác CNF
có góc E1 = góc F1 = 900 (gt)
BM = CN (gt)
góc M = góc N (cmt)
=> t/giác BME = t/giác CNF (cạnh huyền - góc nhọn)
c,d) tự làm

a: Xet ΔABC vuông tại A và ΔBAD vuông tại B có
AB chung
AC=BD
Do đó: ΔABC=ΔBAD
b: Xét tứ giác ABDC có
AC//BD
AC=BD
Do đó; ABDC là hình bình hành
=>AD cắt BC tại trung điểm của mỗi đường
=>EA=ED
c: Xét tứ giác AMDN có
AM//DN
AN//MD
Do đó:AMDN là hình bình hành
=>DN=MA
1/ Xét tg vuông BEA và tg vuông BEM có
BE chung; \(\widehat{ABE}=\widehat{MBE}\Rightarrow\Delta BEA=\Delta BEM\) (Hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau)
2/
\(\Delta BEA=\Delta BEM\Rightarrow BA=BM\) => tg BAM cân tại B \(\Rightarrow BE\perp AM\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
3/ Xét tg vuông AEN và tg vuông MEC có
\(\Delta BEA=\Delta BEM\Rightarrow AE=ME\)
\(\widehat{AEN}=\widehat{MEC}\) (góc đối đỉnh)
\(\Rightarrow\Delta AEN=\Delta MEC\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) \(\Rightarrow AN=MC\)
4/ Ta có
BA=BM; AN=MC (cmt) => BA+AN=BM+MC => BN=BC => tg BNC cân tại B
Mà \(\widehat{ABE}=\widehat{MBE}\)
\(\Rightarrow BE\perp NC\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Ta có \(BE\perp AM\left(cmt\right)\)
=> AM // NC (cùng vuông góc với BE)