Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔBAM cân tại B
mà BE là đường cao
nên BE là phân giác của góc ABM
b: Xét ΔMBA có
AH,BE là đừog cao
AH căt BE tại K
=>K là trực tâm
=>MK vuông gócAB
=>MK//AC

Xét tam giác ABE và tam giác MBE
có BA=BM(GT)
BE chung
AE=EM (GT)
suy ra tam giác ABE = tam giác MBE (c.c.c)
suy ra góc BEA=góc BEM , góc BAE=góc BME (1)
Mà góc BEA + góc BEM=180độ
suy ra góc BEA =góc BEM=90độ
Xét tam giác EAK và tam giác EMK
có AE=EM (GT)
góc KEA=góc KEM = 90 độ
cạnh EK chung
suy ra tam giác EAK = tam giác EMK (cg.c)
suy ra góc KME=góc KAE (2)
Từ (1) và (2) suy ra góc KME +góc EMB=góc KAE+ góc EAB
suy ra góc KMB=góc KAB = 90 độ
suy ra KM vuông góc với BC
c) sai đề nhé

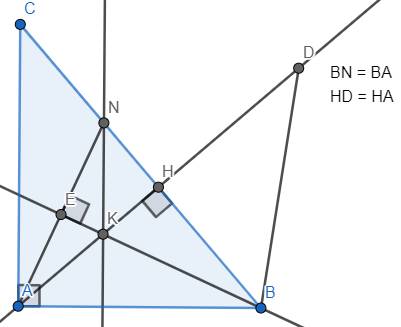
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a, Xét △BAH vuông tại H và △CAH vuông tại H
Có: AH là cạnh chung
AB = AC (gt)
=> △BAH = △CAH (ch-cgv)
=> BH = CH (2 cạnh tương ứng)
Mà H nằm giữa B, C
=> H là trung điểm BC
Ta có: BH + CH = BC => BH + BH = 12 => 2BH = 12 => BH = 6 (cm)
Xét △BAH vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> AH2 = AB2 - BH2
=> AH2 = 102 - 62
=> AH2 = 64
=> AH = 8 (cm)
b, Ta có: MH = MB + BH và HN = HC + CN
Mà BH = HC (cmt) ; MB = CN (gt)
=> MH = HN
Xét △MHA vuông tại H và △NHA vuông tại H
Có: AH là cạnh chung
MH = HN (cmt)
=> △MHA = △NHA (2cgv)
=> HMA = HNA (2 góc tương ứng)
Xét △AMN có: AMN = ANM (cmt) => △AMN cân tại A
c, Xét △MBE vuông tại E và △NCF vuông tại F
Có: EMB = FNC (cmt)
MB = CN (gt)
=> △MBE = △NCF (ch-gn)
=> MBE = NCF (2 góc tương ứng)
d, Vì △MHA = △NHA (cmt) => MAH = NAH (2 góc tương ứng)
=> AH là phân giác của MAN
Ta có: AE + EM = AM và AF + FN = AN
Mà EM = FN (△MBE = △NCF) ; AM = AN (△AMN cân tại A)
=> AE = AF
Xét △EAK vuông tại E và △FAK vuông tại F
Có: AK là cạnh chung
AE = AF (cmt)
=> △EAK = △FAK (ch-cgv)
=> EAK = FAK (2 góc tương ứng)
=> AK là phân giác EAF => AK là phân giác MAN
Mà AH là phân giác của MAN
=> AK ≡ AH
=> 3 điểm A, H, K thẳng hàng
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)