Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left|\overrightarrow{BC}\right|=BC=\sqrt{AB^2+AC^2}=5\)

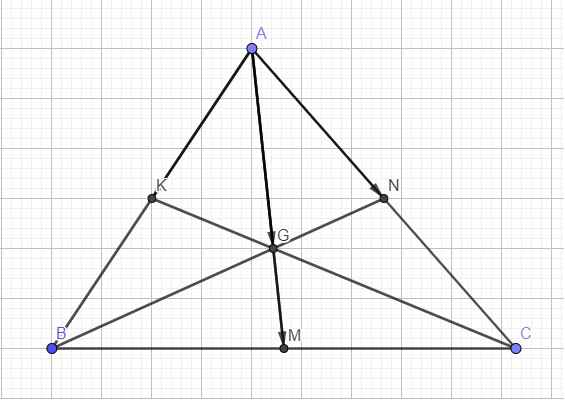
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)

Lời giải:
\(\overrightarrow{a}=-2\overrightarrow{i}+3\overrightarrow{j}=-2(1,0)+3(0,1)=(-2.1+3.0, -2.0+3.1)=(-2,3)\)

ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>AB=CD=2a; BC=AD
O là trung điểm của AC
=>\(AC=2\cdot AO=2a\cdot\sqrt{5}\)
=>\(BD=2a\sqrt{5}\)
ABCD là hình chữ nhật
=>ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=AC^2-AB^2=\left(2a\sqrt{5}\right)^2-\left(2a\right)^2=20a^2-4a^2=16a^2\)
=>BC=4a
=>\(\left|\overrightarrow{BC}\right|=4a\)

a) | MA+MB|=|MA+MC|
gọi I là trung điểm của đoạn AB=> IA+ IB=0
gọi J là trung điểm của đoạn AC=> JA+ JC=0
|MI|=|MJ|
=> M thuộc đường trung trực của đoạn thẳng IJ
b) | MA+ MB+ MC|= |MA-MB|
gọi G là trọng tâm của tam giác ABC=> GA+GB+GC=0
| 3MG|= | BA|
|MG|= 1/3|BA|
=> M thuộc đường tròn tâm G bán kính = 1/3 BA
không có gì đâu bạn. chúc bạn học tốt