
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
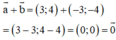
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
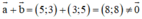
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

a) Vẽ trục và biểu diễn các điểm

b) Ta có:
A có tọa độ là –1, B có tọa độ là 2 nên 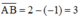
M có tọa độ là 3, N có tọa độ là –2 nên 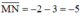


a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi 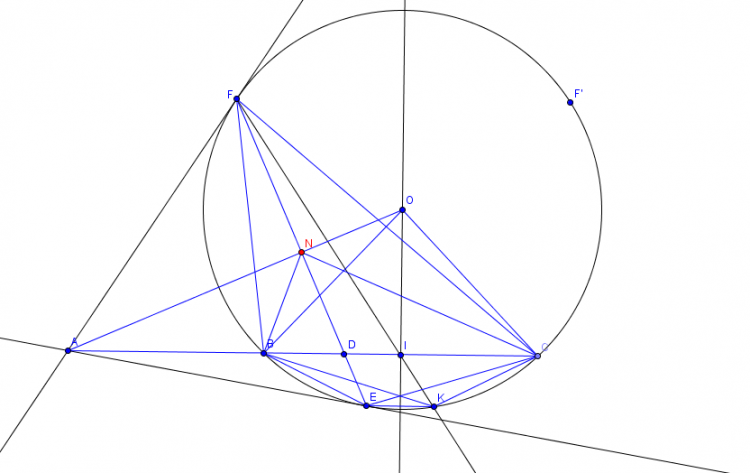
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
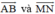 . Từ đó suy ra hai vec tơ
. Từ đó suy ra hai vec tơ 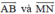 ngược hướng.
ngược hướng.
Hai véc tơ đối nhau.