Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

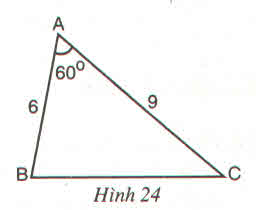
Hình vẽ minh họa như sau:
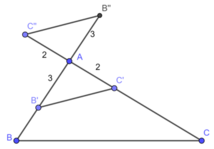
• Cách dựng tam giác AB’C’
- Trên đoạn AB lấy điểm B’ sao cho AB’ = 3cm
- Trên đoạn AC lấy điểm C’ sao cho AC’ = 2cm
- Nối B’ và C’ ta được tam giác AB’C’ là tam giác cần dựng
• Cách dựng tam giác AB’’C’’:
- Trên tia đối của tia AB lấy điểm B’’ sao cho AB’’ = 3cm
- Trên tia đối của tia AC lấy điểm C’’ sao cho AC’’ = 2cm
- Nối B’’ và C’’ ta được tam giác AB’’C’’ cũng thỏa mãn yêu cầu của đề bài
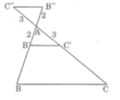
• Cách dựng tam giác AB’C’ đã trình bày ở ý (a)
• Cách dựng tam giác AB’’C’’:
- Trên tia đối của tia AB lấy điểm B’’ sao cho AB’’ = 2cm
- Trên tia đối của tia AC lấy điểm C’’ sao cho AC’’ = 3cm
- Nối B’’ với C’’ ta được tam giác AB’’C’’ thỏa mãn yêu cầu của đề bài.

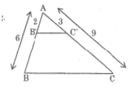
* Cách dựng:
- Trên cạnh AB dựng điểm B' sao cho = 2 cm
- Trên cạnh AC dựng điểm C' sao cho AC' = 3cm
- Nối B'C'
Khi đó AB'C' là tam giác cần dựng
* Chứng minh:
Theo cách dựng, ta có:
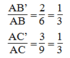
Suy ra: 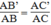
Lại có: ∠ A chung
Vậy △ AB'C' đồng dạng △ ABC (c.g.c)

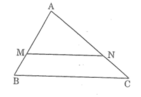
* Cách dựng:
- Trên cạnh AB dựng điểm M sao cho AM = 2/3 AB
- Trên cạnh AC dựng điểm N sao cho AN = 2/3 AC
- Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3
* Chứng minh:
Theo cách dựng ta có:
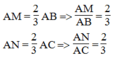
Suy ra: 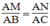
Trong ΔABC, ta có: 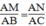
Theo định lí đảo của định lí Ta-lét ta có: MN // BC
Vậy
△
AMN đồng dạng
△
ABC và 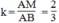

a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(\dfrac{S_{ABC}}{S_{HBA}}=\dfrac{25}{9}\)
nên \(S_{HBA}=24:\dfrac{25}{9}=24\cdot\dfrac{9}{25}=8.64\left(cm^2\right)\)

a/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
BK là pg \(\widehat{ABC}\)
\(\Rightarrow\dfrac{AK}{CK}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=> \(\dfrac{AK}{3}=\dfrac{CK}{5}=\dfrac{AC}{8}=1\)
=> AK = 3cm ; CK = 5 cm
b/ Xét t/g ABC và t/g HBA có
\(\widehat{ABC}\) chung
\(\widehat{BAC}=\widehat{AHB}=90^o\)
=> t/g ABC ~ t/g HBA
=> \(\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
=> \(AB^2=BC.HB\)
c/ \(\dfrac{BC}{AC}=\dfrac{10}{6}=\dfrac{5}{3}\)
t/g ABC ~ t/g HBA vs tỉ số đồng dạng là 5/3