Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



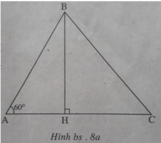
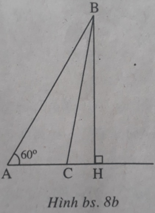
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C


Kẻ \(BH\perp AC\Rightarrow BC^2=BH^2+HC^2=\left(AB^2-AH^2\right)+HC^2\)
\(=AB^2-AH^2+\left(AC-AH\right)^2=AB^2+AC^2-2AC.AH\)
\(\Rightarrow BC^2=AB^2+AC^2-2AC.AB.cos60^0\)
\(\Rightarrow BC^2=AB^2+AC^2-AB.AC\)

a: Xét ΔABE và ΔADC có
\(\widehat{ABE}=\widehat{ADC}\)
\(\widehat{BAE}=\widehat{DAC}\)
Do đó: ΔABE\(\sim\)ΔADC
Suy ra: \(AB\cdot AC=AD\cdot AE\)

Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
Vậy được điều phải chứng minh.