Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
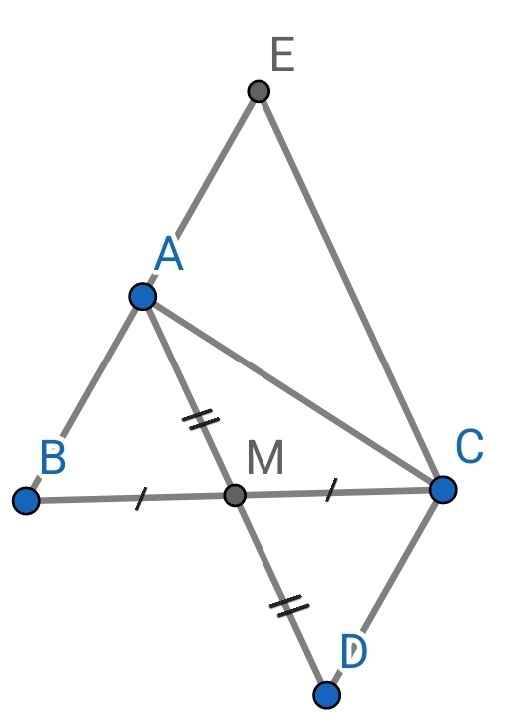a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
a) CM Tam giac ABM = tam giac CDM
Xét tam giac ABM và Tam giác CDM, ta có:
MA = MC (gt)
MB=MD (gt)
Góc AMB = góc DMC (đđ)
Suy ra Tam giác ABM = Tam giác CDM
b) CM AB song song CD
Ta có: Góc MBA =góc MCD ( cmt)
Mà 2 góc này ở vị trí so le trong, nên suy ra AB//CD
c) CM E là trung điểm AC
Ta có: Tứ giác ABCD có:
M là trung điểm AC gt)
M là trung điểm BD (gt)
Mà AC cắt BD tại M
Suy ra: Tứ giac ABCD là hình bình hành
Ta lại có: MN là trung điểm BC , MN //AB//CD.
Do đó NE cũng //AB//CD , và E cũng là trung điểm của AD.
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
DO đó: ΔABM=ΔDCM
=>AB=CD
b: ΔABM=ΔDCM
nên góc ABM=góc DCM
=>AB//CD
c: Xét ΔBEC có
M là trung điểm của BC
MA//EC
Do đó; A là trung điểm của BE
d: Xét tứ giác AECD có
AE//CD
AE=CD
Do đó; AECD là hình bình hành
=>AC cắt ED tại trung điểm của mỗi đường
=>E,I,D thẳng hàng