Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) \(\frac{2x^2-4x+8}{x^3+8}\Rightarrow\) ĐKXĐ: \(x^3+8\ne0 \Leftrightarrow x^3\ne-8 \Leftrightarrow x\ne-2 \)
b) \(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}\Rightarrow f\left(2\right)=\frac{2}{2+2}=\frac{1}{2}\)
d) \(\frac{2}{x+2}=2\)
\(\Leftrightarrow x+2=1\)
\(\Leftrightarrow x=-1\)
uum, mik nghĩ phần C chỗ x+2=1 thì phải gt tại sao x+2=1 thì đúng hơn
a) ĐKXĐ: \(x\ne-2\)
b) Ta có: \(\dfrac{2x^2-4x+8}{x^3+8}\)
\(=\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(=\dfrac{2}{x+2}\)
c) Vì x=2 thỏa mãn ĐKXĐ
nên Thay x=2 vào biểu thức \(\dfrac{2}{x+2}\), ta được:
\(\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi x=2 thì giá trị của biểu thức là \(\dfrac{1}{2}\)
d) Để \(\dfrac{2}{x+2}=2\) thì x+2=1
hay x=-1(nhận)
Vậy: Để \(\dfrac{2}{x+2}=2\) thì x=-1
a, \(ĐKXĐ:x^3+8\ne0\Leftrightarrow x\ne-2\)
b, \(C=\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c, \(\left|2x+1\right|=3\Rightarrow\orbr{\begin{cases}2x+1=3\\2x+1=-3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=-2\left(ktm\right)\end{cases}\Rightarrow x=1}\)
thay vào ta được : \(C=\frac{2}{1+2}=\frac{2}{3}\)
\(\frac{x}{x+2}=2\Leftrightarrow x=2x+4\)
\(\Leftrightarrow x=-4\left(tm\right)\)
a) Phân thức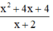 
xác định
⇔ x + 2 ≠ 0
⇔ x ≠ -2
Vậy điều kiện xác định của phân thức là x ≠ -2.
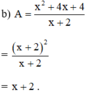
c) A = 1 ⇔ x + 2 = 1 ⇔ x = -1 ≠ -2 (Thỏa mãn điều kiện)
Vậy với x = -1 thì A = 1.
d) A = 0 ⇔ x + 2 = 0 ⇔ x = -2 (Không thỏa mãn điều kiện)
Vậy không có giá trị nào của x để A = 0.
a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .
Câu a :
Để biểu thức được xác định khi \(x+2\ne0\Leftrightarrow x\ne-2\)
Câu b :
\(\dfrac{x^2+4x+4}{x+2}=\dfrac{\left(x+2\right)^2}{x+2}=x+2\)
Câu c :
Để phân thức bằng 1 thì \(x+2=1\Leftrightarrow x=-1\)
Câu d :
Để biểu thức bằng 0 thì \(\left(x+2\right)^2=0\Leftrightarrow x=-2\) ( không thõa mãng )
Nên ko có giá trị x nào hết
a) ĐKXĐ : x+2≠0 ⇒x ≠ -2
b) \(\dfrac{x^{2^{ }}+4x+4}{x+2}\)= \(\dfrac{\left(x+2\right)^2}{x+2}\)= x+2
c) x+2= 1
⇒ x = -1
d) có x = -2 thì giá trị của phân thức = 0
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
bài1 A=\(\left(\frac{3-x}{x+3}\cdot\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(\left(-\frac{x-3\cdot\left(x+3\right)^2}{\left(x+3\right)^2\cdot\left(x-3\right)}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(-\frac{x}{x+3}\cdot\frac{x+3}{3x^2}=\frac{-1}{3x}\)
b) thế \(x=-\frac{1}{2}\)vào biểu thức A
\(-\frac{1}{3\cdot\left(-\frac{1}{2}\right)}=\frac{2}{3}\)
c) A=\(-\frac{1}{3x}< 0\)
VÌ (-1) <0 nên 3x>0
x >0
a. \(x\ne5\) là ĐKXĐ của biểu thức P
b. P =\(\dfrac{\left(x-5\right)^2}{x-5}\)=\(x-5\)
c. P = -1 <=> x-5 =-1 <=> x=4
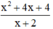
a) ĐKXĐ: \(x^3+8\ne0\Leftrightarrow x^3\ne-8\Leftrightarrow x\ne-2\)
b) \(\dfrac{2x^2-4x+8}{x^3+8}=\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\dfrac{2}{x+2}\)
c) Với x = 2 (t/m ĐKXĐ) ta có
\(\dfrac{2}{2+2}=\dfrac{1}{2}\)
d) \(\dfrac{2}{x+2}=2\)
\(\Leftrightarrow2\left(x+2\right)=2\)
\(\Leftrightarrow2x+4=2\)
\(\Leftrightarrow x=-1\) (t/m ĐKXĐ)
a)tìm điều kiện của x để giá trị của phân thức xác định
ĐKXĐ: x ≠ -2
b) rút gọn
\(\dfrac{2x^2-4x+8}{x^3+8}\)
= \(\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)
= \(\dfrac{2}{x+2}\)
c) giá trị của phân thức tại x=2:
thay x=2 , ta được:
\(\dfrac{2}{x+2}=\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
d)
Tìm giá trị của x để giá trị của phân thức = 2:
\(\dfrac{2}{x+2}=2\)
<=> \(\dfrac{2}{x+2}=\dfrac{2\left(x+2\right)}{x+2}\)
=> 2 = 2(x + 2)
<=> 2 = 2x +4
<=> 2x = 2 - 4
<=> 2x = - 2
<=> \(\dfrac{2x}{2}=\dfrac{-2}{2}\)
<=> \(x=-1\)
Vậy để giá trị của phân thức bằng 2 thì giá trị của x là -1