Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Phân thức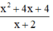 
xác định
⇔ x + 2 ≠ 0
⇔ x ≠ -2
Vậy điều kiện xác định của phân thức là x ≠ -2.
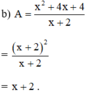
c) A = 1 ⇔ x + 2 = 1 ⇔ x = -1 ≠ -2 (Thỏa mãn điều kiện)
Vậy với x = -1 thì A = 1.
d) A = 0 ⇔ x + 2 = 0 ⇔ x = -2 (Không thỏa mãn điều kiện)
Vậy không có giá trị nào của x để A = 0.
Lời giải:
a. ĐKXĐ: $x^2-16\neq 0\Leftrightarrow (x-4)(x+4)\neq 0$
$\Leftrightarrow x\neq \pm 4$
b. $A=\frac{x^2+8x+16}{x^2-16}=\frac{(x+4)^2}{(x-4)(x+4)}=\frac{x+4}{x-4}$
c. $A=3\Leftrightarrow \frac{x+4}{x-4}=3$
$\Rightarrow x+4=3(x-4)$
$\Leftrightarrow -2x+16=0$
$\Leftrightarrow x=8$ (tm)
d.
$A=0\Leftrightarrow \frac{x+4}{x-4}=0\Leftrightarrow x+4=0\Leftrightarrow x=-4$
Mà theo ĐKXĐ thì $x\neq \pm 4$ nên không tồn tại $x$ để $A=0$
a)ĐKXĐ:
\(x+2\ne0\Leftrightarrow x\ne-2\)
b)\(\frac{x^2+4x+4}{x+2}=\frac{\left(x+2\right)^2}{x+2}=x+2\)
c)\(\text{Để phân thức =0 thì x+2=0},\text{mà x+2}\ne0\text{,nên ko có giá trị nào của để phân thức =0}\)
\(\frac{x^2+4x+4}{x+2}\)
a/ Để phân thức đc xác định thì x + 2 \(\ne\) 0 => x \(\ne\) -2
Vậy để phân thức đc xác định thì x \(\ne\) -2
b/ \(\frac{x^2+4x+4}{x+2}=\frac{\left(x+2\right)^2}{x+2}=x+2\)
c/ Để phân thức bằng 0 thì x + 2 = 0 => x = -2 (loại)
Vậy không có giá trị nào của x để phân thức = 0
Câu a :
Để biểu thức được xác định khi \(x+2\ne0\Leftrightarrow x\ne-2\)
Câu b :
\(\dfrac{x^2+4x+4}{x+2}=\dfrac{\left(x+2\right)^2}{x+2}=x+2\)
Câu c :
Để phân thức bằng 1 thì \(x+2=1\Leftrightarrow x=-1\)
Câu d :
Để biểu thức bằng 0 thì \(\left(x+2\right)^2=0\Leftrightarrow x=-2\) ( không thõa mãng )
Nên ko có giá trị x nào hết
a) ĐKXĐ : x+2≠0 ⇒x ≠ -2
b) \(\dfrac{x^{2^{ }}+4x+4}{x+2}\)= \(\dfrac{\left(x+2\right)^2}{x+2}\)= x+2
c) x+2= 1
⇒ x = -1
d) có x = -2 thì giá trị của phân thức = 0
a. \(x\ne5\) là ĐKXĐ của biểu thức P
b. P =\(\dfrac{\left(x-5\right)^2}{x-5}\)=\(x-5\)
c. P = -1 <=> x-5 =-1 <=> x=4
a) \(\frac{2x^2-4x+8}{x^3+8}\Rightarrow\) ĐKXĐ: \(x^3+8\ne0 \Leftrightarrow x^3\ne-8 \Leftrightarrow x\ne-2 \)
b) \(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}\Rightarrow f\left(2\right)=\frac{2}{2+2}=\frac{1}{2}\)
d) \(\frac{2}{x+2}=2\)
\(\Leftrightarrow x+2=1\)
\(\Leftrightarrow x=-1\)
uum, mik nghĩ phần C chỗ x+2=1 thì phải gt tại sao x+2=1 thì đúng hơn
a) ĐKXĐ: \(x\ne-2\)
b) Ta có: \(\dfrac{2x^2-4x+8}{x^3+8}\)
\(=\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(=\dfrac{2}{x+2}\)
c) Vì x=2 thỏa mãn ĐKXĐ
nên Thay x=2 vào biểu thức \(\dfrac{2}{x+2}\), ta được:
\(\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi x=2 thì giá trị của biểu thức là \(\dfrac{1}{2}\)
d) Để \(\dfrac{2}{x+2}=2\) thì x+2=1
hay x=-1(nhận)
Vậy: Để \(\dfrac{2}{x+2}=2\) thì x=-1
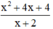
a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .