Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét phương trình hoành độ giao điểm: x2 – 2x + m – 1 = 0
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương thì phương trình có hai nghiệm dương hay 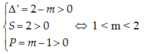
Chọn A.

Xét phương trình hoành độ giao điểm: x2 + x+ 2 = ax + 1
x2 + (1 – a) x + 1 = 0
Để (P) tiếp xúc với (d) thì phương trình có nghiệm kép hay
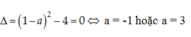
Chọn A.

Phương trình hoành độ giao điểm: - x 2 + 2 x + 3 = m x ⇔ x 2 + m - 2 x - 3 = 0 1
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì a c = 1 . - 3 = - 3 < 0
Khi đó (d) cắt (P) tại hai điểm phân biệt A x 1 ; m x 1 , B x 2 ; m x 2 , với x 1 , x 2 là nghiệm phương trình (1). Theo Viét, có: x 1 + x 2 = 2 - m , x 1 x 2 = - 3 x 1 x 2 = - 3
I là trung điểm
A B ⇒ I = x 1 + x 2 2 ; m x 1 + m x 2 2 = 2 − m 2 ; − m 2 + 2 m 2
Mà I ∈ ( Δ ) : y = x − 3 ⇒ − m 2 + 2 m 2 = 2 − m 2 − 3 ⇔ m 2 − 3 m − 4 = 0
⇔ m = − 1 = m 1 m = 4 = m 2 ⇒ m 1 + m 2 = 3
Đáp án cần chọn là: D

Phương trình hoành độ giao điểm là:
\(x^2-2\left(m-1\right)x+m^2-m=0\)
\(\Delta=\left(2m-2\right)^2-4\left(m^2-m\right)\)
\(=4m^2-8m+4-4m^2+4m=-4m+4\)
Để (P) cắt Ox tại 2 điểm phân biệt thì \(\Delta>0\)
=>-4m+4>0
=>-4m>-4
=>m<1

Xét ptr hoành độ của `(d)` và `(P)` có:
`(m-1)x^2+2mx+3m-1=2x+m`
`<=>(m-1)x^2+2(m-1)x+2m-1=0` `(1)`
`(d)` tiếp xúc `(P)<=>` Ptr `(1)` có nghiệm kép
`<=>{(a \ne 0),(\Delta'=0):}`
`<=>{(m-1 \ne 0),((m-1)^2-(m-1)(2m-1)=0):}`
`<=>{(m \ne 1),(-m(m-1)=0):}`
`<=>m=0`
`->B`
Phương trình hoành độ giao điểm : \(m-1x2+2mx+3m-1=2x+m\)
\(\Leftrightarrow m-1x2+2m-1x+2m-1=0\)
Để d tiếp xúc với P khi và chỉ khi phương trình có nghiệm kép
\(\Leftrightarrow m-1\ne0\Delta'=m-15-m-12m-1=-mm-1=0\) \(\Leftrightarrow m\ne1m=0m=1\Leftrightarrow m=0\)
\(\Rightarrow\) chọn \(B\)

Phương trình hoành độ giao điểm là:
\(x^2+\left(m+2\right)x+m-2x+3=0\)
\(\Leftrightarrow x^2+mx+m+3=0\)
Để (P) cắt (d) tại hai điểm nằm về hai phía với trục tung thì m+3<0
hay m<-3


Xét phương trình hoành độ giao điểm:
x2 – 2x + m – 1 = 0 tương đương (x – 1)2 = 2 – m (1)
Để parabol không cắt trục Ox thì phương trình (1) vô nghiệm hay 2 – m < 0 hay m > 2
Chọn B.