Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mỗi giao điểmcủa hai đường chéoứng với một và chỉ một tập hợp gồm 4 điểmtừ tập hợp 7 đỉnh của đa giác. Vậy có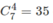 
giao điểm.
Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là 
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
tham khảo
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là C210C102
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
Với mỗi bộ 4 đỉnh của đa giác ta có đúng hai đường chéo của đa giác mà giao điểm của chúng nằm trong đa giác.
Do đó số giao điểm cần tìm là 
.
Chọn A
Xét 1 đỉnh bất kì nối tới 17 đỉnh (trừ ra 2 đỉnh kề với đỉnh đang xét) ta đc 17 đường chéo.
Có 20 đỉnh suy ra có :
20.17=340 (đường chéo)
Nhưng như thế mỗi đường chéo ta đã được tính 2 lần .
Vậy số đường chéo trong 1 đa giác lồi 20 cạnh là :
340 : 2=170 (đường chéo)
a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 thẻ trong số 6 thẻ.
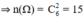
a. Gọi A: “ Hai điểm là đầu mút của cạnh của lục giác”
⇒ n(A) = 6 (Lục giác có 6 cạnh)
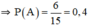
b. Gọi B: “ Hai điểm là đầu mút của đường chéo”
⇒ B = A− (Vì một đoạn thẳng chỉ có thể là một cạnh hoặc một đường chéo)
⇒ P(B) = 1 – P(A) = 1 – 0,4 = 0,6
c. Gọi C: “ Hai điểm là đầu mút của đường chéo nối hai đỉnh đối diện”
⇒ n(C) = 3
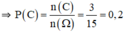
Mỗi giao điểm của hai đường chéo ứng với một và chỉ một tập hợp gồm 4 điểm từ tập hợp 7 đỉnh của đa giác.
Vậy có \(C^4_7=35\) giao điểm