Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là
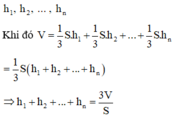
Đáp án A
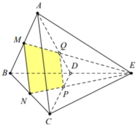
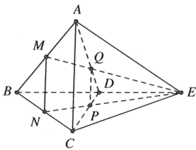
Nối 
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích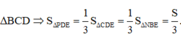 
Họi h là chiều cao của tứ diện ABCD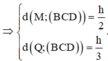 
Khi đó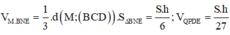 
Suy ra
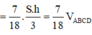
Chọn đáp án D
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD:
FOR REVIEW |
Tam giác cân có một góc bằng 60 ° thì là tam giác đều. |
Đáp án B
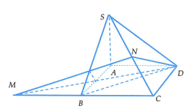
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC’ và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa mãn yêu cầu bài toán.
Ta có d I ; A ' B ' C ' D ' = d I ; B C C ' B ' = d I ; D C C ' D '
Suy ra I thuộc đoạn thẳng C’M và mặt cầu tâm I cần tìm đi qua điểm M.
Đặt d I ; D C C ' D ' = a , ta có IC' = a 3 mà A C ' = 3 3 , A M = 3
Suy ra I M = 2 3 - a 3 mặt khác d I ; D C C ' D ' = I M ⇔ a = 2 3 - a 3 ⇒ a = 3 - 3 3
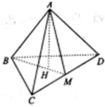
Chọn B.
Gọi x, y, z, t lần lượt là khoảng cách từ M đến các mặt phẳng (BCD), (CDA), (DAB), (ABC). Ta có
Cộng lại ta thu được (chú ý rằng)
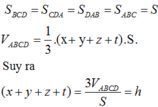
với h là độ dài đường cao của tứ diện đều ABCD. Ta có
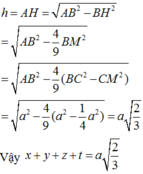
Chọn đáp án C
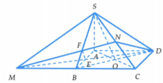
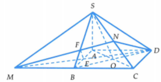
Gọi O là giao điểm của AC và BD
Ta có
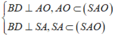
⇒ Thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (MND) là tứ giác DEFN.
Suy ra V 1 = V S . A D E F N và V 2 = V B C D E F N
Từ giả thiết ta có ∆ A B D đều cạnh a
Thể tích khối chóp N.MCD là
V N . M C D = 1 3 d N ; M C D . S ∆ M C D = a 3 4
Ta có F là trọng tâm của ∆ S M C nên M F M N = 2 3 ; E là trung điểm của MD nên M E M D = 1 2
Áp dụng công thức tính thể tích ta có:
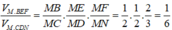
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S A B C D = a 3 4
Suy ra V 1 = V S . A D E F N = V S . A B C D - V 2 = a 3 24
Vậy V 1 V 2 = 1 5
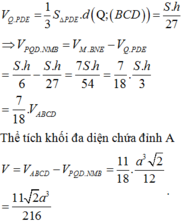
Đáp án A
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là h 1 , h 2 , . .. , h n n
Khi đó