Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

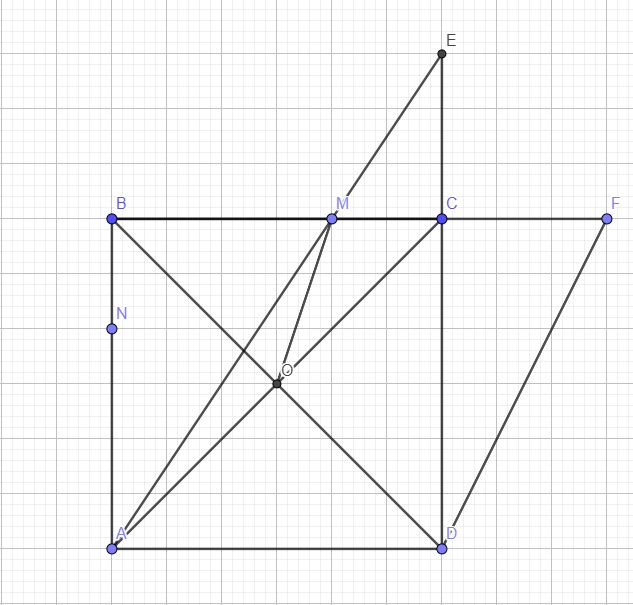
Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

1: Xét ΔCAB có
D,E lần lượt là trung điểm của BA,BC
=>DE là đường trung bình của ΔCAB
=>DE//AC
DE//AC
AB\(\perp\)AC
Do đó: DE\(\perp\)AB
AB=2AC
AB=2AD=2BD
Do đó: AD=BD=AC
Xét tứ giác ADFC có
\(\widehat{CFD}=\widehat{CAD}=\widehat{ADF}=90^0\)
=>ADFC là hình chữ nhật
Hình chữ nhật ADFC có AC=AD
nên ADFC là hình vuông

a) Ta chứng minh:
S A E F = S A B C D = 1 4 S A B F
b) Từ câu a suy ra EH = CK
c) Gọi SBDE = S1; SADE = S2;
Ta chứng minh DE = DC;
Ta tính được:
ABDC = S1; SADC = S2, suy ra SABC = 2(S1 + S2) = 2.SABD

a: Xét ΔABF vuông tại B và ΔADE vuông tại D có
AB=AD
BF=DE
Do đó: ΔABF=ΔADE
=>\(\widehat{BAF}=\widehat{DAE}\)
mà \(\widehat{DAE}+\widehat{EAB}=90^0\)
nên \(\widehat{BAF}+\widehat{BAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Ta có: ΔABF=ΔADE
=>AF=AE
Xét ΔAFE có AF=AE và \(\widehat{FAE}=90^0\)
nên ΔAFE vuông cân tại A
b: Bạn ghi lại đề đi bạn