Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


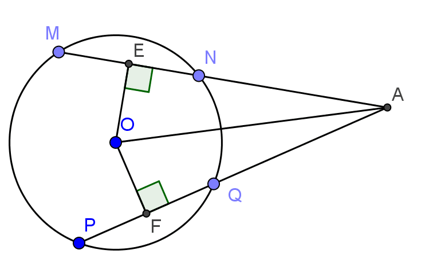
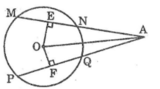
Ta có: OE ⊥ MN (gt)
Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung) (1)
OF ⊥ PQ (gt)
Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung) (2)
Mặt khác: MN = PQ (gt) (3)
Từ (1), (2) và (3) suy ra: EN = FQ (4)
Mà AE = QF (chứng minh trên) (5)
Từ (4) và (5) suy ra: AN + NE = AQ + QF (6)
Từ (5) và (6) suy ra: AN = AQ

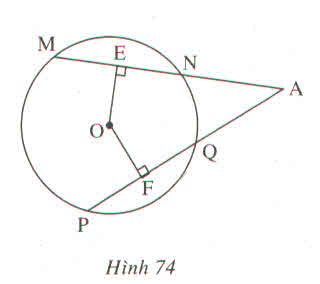
Nối OA
Ta có: MN = PQ (gt)
Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OAE và OAF, ta có:
![]()
OA chung
OE = OF (chứng minh trên)
Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)
Suy ra: AE = AF

:v nếu hưng thấy thì hưng cũm có thể giúp nhưn mà k thấy thì chịu nhá
Tứ giác AMSQ có: AM // SQ ; MS // AQ} gt
⇔ Tứ giác AMSQ là hình bình hành ⇒ AM = SQ
Tứ giác BWSP có: BW // SP ; BP // WS} gt
⇔ Tứ giác BWSP là hình bình hành ⇒ BW = SP
Tứ giác GSLK có: GK // SL ; GS // KL} gt
⇔ Tứ giác GSLK là hình bình hành ⇒ GK = LS
+) \(SQ + SP = PQ(gt) \) trong khi \(AM = SQ ;BW = SP \)
\(⇔ AM + BW = SQ + SP = PQ\)
+) \(2GK + WS = WS + SL + GK\) (vì GK = LS) \(= WL + GK\)
Vì ▲ABK có MG // AK; WL // BK và M,W ∈ AB; G ∈ BK; L ∈ AK nên:
\(+)\frac{WL}{BK} = \frac{AW}{AB} \) (Định lý Talet)
\(+)\frac{BG}{BK} = \frac{MB}{AB}\) (Định lý Talet) \(⇔\frac{BK - GK}{BK} = \frac{AB - AM}{AB}\)
\(⇔ 1 – \frac{GK}{BK} = 1 – \frac{AM}{AB} \)
\(⇔ \frac{GK}{BK} = \frac{AM}{AB}\)
Vì ▲ABK có PQ // AB và P ∈ BK; Q ∈ AK nên: \(+) \frac{QK}{AK} = \frac{PQ}{AB} \) (Định lý Talet)
\(⇔1 – \frac{QK}{AK} = 1 – \frac{PQ}{AB}\)
\(⇔ \frac{AK-QK}{AK} = \frac{AB-PQ}{AB} \)
\(⇔ \frac{AQ}{AK} = \frac{AB-PQ}{AB}\)
\(+) 2(\frac{BW}{AB}+\frac{GK}{BK})+\frac{WS}{BK}+\frac{AQ}{AK} = \frac{2BW}{AB}+\frac{2GK}{BK}+\frac{WS}{BK}+\frac{AQ}{AK} \)
\( = \frac{2BW}{AB}+\frac{WL + GK}{BK}+\frac{AQ}{AK}\)
Với \(\frac{GK}{BK} = \frac{AM}{AB} ; \frac{WL}{BK} = \frac{AW}{AB}; \frac{AQ}{AK} = \frac{AB-PQ}{AB}\) , ta có:
\(\frac{2BW}{AB}+\frac{WL}{BK}+\frac{GK}{BK}+\frac{AQ}{AK} \)
\(= \frac{BW + BW}{AB}+\frac{AW}{AB}+\frac{AM}{AB}+\frac{AB - PQ}{AB}\)
\(= \frac{AB + BW + AW + AM + BW – PQ}{AB}\)
\(= \frac{AB + AB + PQ – PQ}{AB} \)
\(= \frac{2AB}{AB} = 2\)
➤ \(2(\frac{BW}{AB}+\frac{GK}{BK})+\frac{WS}{BK}+\frac{AQ}{AK}\) \(=2\)