K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
ND
Nguyễn Đức Quang
8 tháng 7 2018 - olm

Cho hình vẽ sau, trong đó MN=PQ. Chứng minh rằng:

a, AE=AF

b, AN=AQ.

Chuyên đề Toán lớp 9
#Toán lớp 9
0
PT
Pham Trong Bach
7 tháng 6 2019

Cho hình bên, trong đó MN = PQ. Chứng minh rằng: AN = AQ
#Toán lớp 9
1
CM
Cao Minh Tâm
7 tháng 6 2019

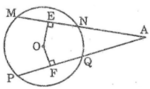
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Ta có: OE ⊥ MN (gt)

Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung)     (1)

OF ⊥ PQ (gt)

Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung)     (2)

Mặt khác: MN = PQ (gt)     (3)

Từ (1), (2) và (3) suy ra: EN = FQ     (4)

Mà AE = QF (chứng minh trên)     (5)

Từ (4) và (5) suy ra: AN + NE = AQ + QF     (6)

Từ (5) và (6) suy ra: AN = AQ

Đúng(0)
PT
Pham Trong Bach
15 tháng 5 2019

Cho hình bên, trong đó MN = PQ. Chứng minh rằng: AE = AF
#Toán lớp 9
1
CM
Cao Minh Tâm
15 tháng 5 2019

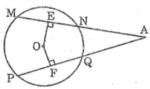
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Nối OA

Ta có: MN = PQ (gt)

Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)

Xét hai tam giác OAE và OAF, ta có: 

Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

OA chung

OE = OF (chứng minh trên)

Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)

Suy ra: AE = AF

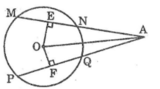
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)
TT
Thầy Tùng Dương
VIP
9 tháng 4 2021 - olm
Cho một điểm A ở ngoài đường tròn (O). Kẻ hai cát tuyến AMN và APQ tới đường tròn sao cho MN > PQ. Dựng đường tròn (O ; OA). Kẻ hai dây AD và AF của đường tròn lớn tiếp xúc với đường tròn nhỏ tại B và C. Cát tuyến AMN và cát tuyến APQ cắt đường tròn lớn ở E và H. a) Chứng minh AD = AF; b) Chứng minh AE > AH; c) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn; d) So sánh...
Đọc tiếp

Cho một điểm A ở ngoài đường tròn (O). Kẻ hai cát tuyến AMN và APQ tới đường tròn sao cho MN > PQ. Dựng đường tròn (O ; OA). Kẻ hai dây AD và AF của đường tròn lớn tiếp xúc với đường tròn nhỏ tại B và C. Cát tuyến AMN và cát tuyến APQ cắt đường tròn lớn ở E và H.

a) Chứng minh AD = AF;

b) Chứng minh AE > AH;

c) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn;

d) So sánh $\widehat{OAE}$ và $\widehat{OAH}$.
#Toán lớp 9
12
NN
Nhật Nam
22 tháng 8 2021

a) AD và AF cách đều tâm O nên chúng bằng nhau.

b) Kẻ OI ⊥ MN, OK ⊥ PQ.

Trong đường tròn nhỏ, ta có: MN > PQ ⇒ OI < OK.

(Dây lớn hơn thì gần tâm hơn)

Trong đường tròn lớn, OI < OK ⇒ AE > AH.

(Dây gần tâm hơn thì lớn hơn)

c) A, B, O, C cách đều trung điểm AO.

d) OI<OK⇒OIOA<OKOA

Đúng(0)
PV
Phương Vy
22 tháng 8 2021

a) AD và AF cách đều tâm O nên chúng bằng nhau.

b) Kẻ OI \bot MN, OK \bot PQ.

Trong đường tròn nhỏ, ta có: MN > PQ \Rightarrow OI < OK.

(Dây lớn hơn thì gần tâm hơn)

Trong đường tròn lớn, OI < OK \Rightarrow AE > AH.

(Dây gần tâm hơn thì lớn hơn)

c) A, B, O, C cách đều trung điểm AO.

d) OI < OK\Rightarrow\frac{OI}{OA}<\frac{OK}{OA}

\Rightarrow \sin{\widehat{OAI}}< \sin{\widehat{OAK}} \Rightarrow \widehat{OAI}<\widehat{OAK} \Rightarrow \widehat{OAE}<\widehat{OAH}.

Đúng(0)
LS
Lê Song Phương
27 tháng 2 2022 - olm

Cho \(\Delta ABQ\)vuông tại A với \(AB=1\). Trên cạnh AQ lấy 3 điểm M, N, P sao cho \(AM< AN< AP\), biết rằng \(4AM+3MN+2NP+PQ=4\). Chứng minh rằng \(\frac{AM}{BN^2}+\frac{AN}{BP^2}+\frac{AP}{BQ^2}+\frac{AQ}{BM^2}\ge2\)
#Toán lớp 9
0
NT
Nguyễn Tất Đạt
16 tháng 7 2018 - olm
Cho đường tròn (O;R). Từ 1 điểm A nằm ngoài đường tròn kẻ 2 tiếp tuyến AP và AQ (P và Q là 2 tiếp điểm). Đường thẳng d bất kỳ nằm ngoài đường tròn cắt AP và AQ lần lượt tại E và F. Trên nửa mặt phẳng bờ EF chứa điểm A vẽ tia Ex sao cho \(\widehat{FEx}=\widehat{AEO}\), tia này giao tia AO tại G. H là hình chiếu vuông góc của G lên EF. Qua H kẻ đường thẳng vuông góc với PQ ở K, đường...
Đọc tiếp

Cho đường tròn (O;R). Từ 1 điểm A nằm ngoài đường tròn kẻ 2 tiếp tuyến AP và AQ (P và Q là 2 tiếp điểm). Đường thẳng d bất kỳ nằm ngoài đường tròn cắt AP và AQ lần lượt tại E và F. Trên nửa mặt phẳng bờ EF chứa điểm A vẽ tia Ex sao cho \(\widehat{FEx}=\widehat{AEO}\), tia này giao tia AO tại G. H là hình chiếu vuông góc của G lên EF. Qua H kẻ đường thẳng vuông góc với PQ ở K, đường thẳng này cắt AE và AF tại M và N.

a) Chứng minh: \(\Delta MAN\)là tam giác cân ?

b) Chứng minh \(\widehat{EFG}=\widehat{AFO}\)?

c) Chứng minh KH là phân giác của \(\widehat{EKF}\)?
#Toán lớp 9
0
DT
dương thị loan
29 tháng 6 2016 - olm

Cho hình bình hành ABCD, dựng vecto AM = vecto BA, vecto MN = vecto DA, vecto NP = vecto DC, vecto PQ = vecto BC. chứng minh vecto AQ bằng vecto không

  •  

 
#Toán lớp 9
0
TT
tram thai thinh
13 tháng 2 2023

Cho nửa đường tròn (O;R) và hai đường kính MN và PQ vuông góc với nhau.Lấy điểm A trên cung nhỏ PN,PA cắt MN tại B,AQ cắt MN tại E.

a)Chứng minh tứ giác OABQ là tứ giác nội tiếp

b)Nối AM cắt BQ và PN lần lượt tại C và I.Chứng minh MC.MA không đổi khi A di chuyển trên cung nhỏ PN
#Toán lớp 9
0
N
nguyenthithuytien
23 tháng 9 2017 - olm

Cho tam giác ABC gọi P là trung điểm của BC; AE và AF thứ tự là đường phân giác trong và ngoài của góc A; H là hình chiếu A lên BC chứng minh rằng EF.DH=AB.AC
#Toán lớp 9
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP