Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

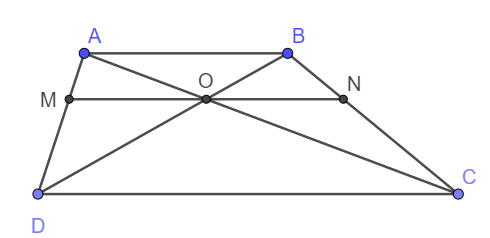
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

a) Xét tam giác ADC có MH//AC nên \(\frac{AM}{MD}=\frac{CH}{HD}\) (Định lý Ta-let)
Lại có theo giả thiết \(\frac{AM}{MD}=\frac{CN}{BN}\)
Suy ra \(\frac{CN}{BN}=\frac{CH}{DH}\)
Xét tam giác DBC có \(\frac{CN}{BN}=\frac{CH}{DH}\) nên áp dụng định lý đảo của định lý Talet ta có HN//BD
b) Gọi giao điểm của MH với BD là G; của AC với NH là K, của OH với GK là J.
Trước hết, ta chứng minh GK//MN.
Thật vậy, do HM // AC nên theo định lý Ta let ta có \(\frac{MG}{GH}=\frac{AO}{OC}\)
Do HN//BD (cma) nên \(\frac{KN}{KH}=\frac{OB}{OD}\)
Mà \(\frac{OB}{OD}=\frac{AO}{OC}\Rightarrow\frac{MG}{GH}=\frac{KN}{KH}\)
Theo định lý Ta lét đảo, suy ra GK//MN.
Xét tứ giác OGHK có GO//HK; GH//OK nên OGHK là hình bình hành
Vậy thì J là trung điểm của EK.
Xét tam giác OGK có EF // GK nên ta có :
\(\frac{EI}{GJ}=\frac{FI}{KJ}\Rightarrow\frac{EI}{GJ}=\frac{FI}{GJ}\Rightarrow EI=FI\)
Ta cũng có GK//MN nên :
\(\frac{GJ}{MI}=\frac{KJ}{IN}\Rightarrow MI=NI\Rightarrow ME=NF\)
giúp em vs CMR với mọi a,b,c ta có (a^2+2)(b^2+2)(c^2+2)>= 3(a+b+c)^2

ta có: góc ACD= góc ABD (vì cùng chắn cung AD nhỏ)
xét tam giác ACG và tam giác DBG có:
góc AGC =góc DGB (2 góc đối đỉnh)
góc ACG= góc DBG (cmt)
=> tam giác AGC ~ tam giác DGB(g-g)
=>\(\frac{AG}{AC}=\frac{DG}{DB}\) \(\Rightarrow\frac{AG}{DG}=\frac{CG}{BG}\)(1)
ta có GM là phân giác góc AGD => \(\frac{AG}{GD}=\frac{AM}{MD}\left(2\right)\)
Ta có: góc CGB = góc AGD (2 góc đối đỉnh)
mà MN là phân giác góc AGD
=> MN là phân giác gócCGB
hay GN là phân giác góc CGB
=> \(\frac{CG}{BG}=\frac{CN}{BN}\)(3)
từ (1);(2) và (3) ta có \(\frac{AM}{MD}=\frac{CN}{NB}\left(đpcm\right)\)