Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét đường tròn (O) có 2 tiếp tuyến NE, NC (E và C là tiếp điểm) => EN = CN (T/c 2 tiếp tuyến giao nhau)
Ta thấy: ^BAC nội tiếp (O), phân giác ^BAC cắt (O) tại điểm thứ hai E => E là điểm chính giữa cung nhỏ BC
=> OE vuông góc với BC. Mà EN vuông góc OE nên EN // BC. Áp dụng ĐL Thales có:
\(\frac{CN}{CD}=\frac{EN}{CD}=\frac{PN}{CP}\)=> \(\frac{CN}{CD}+\frac{CN}{CP}=\frac{PN+CN}{CP}=1\)=> \(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\)(đpcm).

kho..................wa...........................troi.....................thi.....................rer...................lam sao duoc........................huhu.....................tich......................ung.......................ho........................minh..................cai...................cho....................do....................ret
AMB=ANB=90 ( góc nội tiếp chắn nửa đường tròn )=> AN và BM là 2 đường cao => D là trực tâm tam giác ABC => CD vuông AB

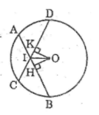
Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)
Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)

a: góc AMB=1/2*sđ cung AB=90 độ
góc FEB+góc FMB=180 độ
=>FMBE nội tiếp
b: Xét ΔKAB có
AM,KE là đường cao
KE cắt AM tại F
=>F là trực tâm
=>BF vuông góc AK
ta có: góc ACD= góc ABD (vì cùng chắn cung AD nhỏ)
xét tam giác ACG và tam giác DBG có:
góc AGC =góc DGB (2 góc đối đỉnh)
góc ACG= góc DBG (cmt)
=> tam giác AGC ~ tam giác DGB(g-g)
=>\(\frac{AG}{AC}=\frac{DG}{DB}\) \(\Rightarrow\frac{AG}{DG}=\frac{CG}{BG}\)(1)
ta có GM là phân giác góc AGD => \(\frac{AG}{GD}=\frac{AM}{MD}\left(2\right)\)
Ta có: góc CGB = góc AGD (2 góc đối đỉnh)
mà MN là phân giác góc AGD
=> MN là phân giác gócCGB
hay GN là phân giác góc CGB
=> \(\frac{CG}{BG}=\frac{CN}{BN}\)(3)
từ (1);(2) và (3) ta có \(\frac{AM}{MD}=\frac{CN}{NB}\left(đpcm\right)\)