Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\Rightarrow\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}\)
Theo Talet: \(\dfrac{A'K}{IK}=\dfrac{B'I}{A'D'}=\dfrac{1}{2}\Rightarrow A'K=\dfrac{2}{3}A'I\)
\(\Rightarrow\overrightarrow{A'K}=\dfrac{2}{3}\overrightarrow{A'I}=\dfrac{2}{3}\left(\overrightarrow{A'B'}+\overrightarrow{B'I}\right)=\dfrac{2}{3}\left(\overrightarrow{A'B'}+\dfrac{1}{2}\overrightarrow{B'C'}\right)\)
\(=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{a}+\dfrac{1}{3}\left(\overrightarrow{b}-\overrightarrow{a}\right)=\dfrac{1}{3}\overrightarrow{a}+\dfrac{1}{3}\overrightarrow{b}\)
\(\Rightarrow\overrightarrow{DK}=\overrightarrow{DD'}+\overrightarrow{D'A'}+\overrightarrow{A'K}=\overrightarrow{AA'}-\overrightarrow{BC}+\overrightarrow{A'K}\)
\(=\overrightarrow{c}-\left(\overrightarrow{b}-\overrightarrow{a}\right)+\dfrac{1}{3}\overrightarrow{a}+\dfrac{1}{3}\overrightarrow{b}\)
\(=\dfrac{4}{3}\overrightarrow{a}-\dfrac{2}{3}\overrightarrow{b}+\overrightarrow{c}\)


a) Tìm giao tuyến của mp(MNO) và mp(DD'B'B).
Gọi L, F, S lần lượt là trung điểm của A'D'; B'C'; BC. Suy ra \(O\in mp\left(NSFL\right)\).
Gọi Q là trung điểm của B'D'. Trong mp(DD'B'B) vẽ đường thẳng d song song với DD'.
Do DD' // NL và Q thuộc LF nên d thuộc mặt phẳng (NSFL). Gọi giao điểm của đường thẳng này với NO là I.
Suy ra \(I\in mp\left(DD'B'B\right)\cap mp\left(NSFL\right)\).
I thuộc NO nên I thuộc mặt phẳng (MON).
Trong mp(DD'B'D) từ I kẻ đường thẳng song song với BD. Gọi giao điểm của đường thẳng này với DD' và BB' là K, H.
Do MN // BD nên KH // MN suy ra KN thuộc mp(MON).
Gọi giao điểm của NO với CC' là T. Vậy thiết diện chính là ngũ giác MNHTK.
2)
Ta tìm giao tuyến của mp(ACC'A') với mặt phẳng (MON).
Trong mp(ADCB) gọi giao điểm của MN với AC là P. Suy ra giao tuyến của mp(ACC'A') với mp(MON) là PT.
Kéo dài PT cắt A'C' tại E chính là giao điểm cần tìm.


\(AH\perp\left(ABCD\right)\Rightarrow\widehat{A'AH}\) là góc giữa AA' và (ABCD) \(\Rightarrow\widehat{A'AH}=60^0\)
\(\Rightarrow AA'=\dfrac{AH}{cos60^0}=a\)
a. Ta có: \(\left\{{}\begin{matrix}A'H\perp\left(ABCD\right)\Rightarrow A'H\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABB'A'\right)\)
Mà \(AD\in\left(ADD'A'\right)\Rightarrow\left(ADD'A'\right)\perp\left(ABB'A'\right)\)
b. Kiểm tra lại đề câu này
Hai mặt phẳng (ABCD) và (A'B'C'D') hiển nhiên song song (theo tính chất lăng trụ) nên góc giữa chúng bằng 0. Do đó thấy ngay \(tan\left(\left(ABCD\right);\left(A'B'C'D'\right)\right)=0\)
Có lẽ không ai bắt tính điều này cả.
c.
\(\left(ABCD\right)||\left(A'B'C'D'\right)\Rightarrow d\left(A;\left(A'B'C'D'\right)\right)=d\left(A';\left(ABCD\right)\right)=A'H=a\)

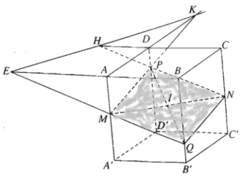
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).

a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB',CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.


Chắc đề đúng là tính \(d\left(A;\left(BCC'B'\right)\right)\)
Gọi E là trung điểm BC \(\Rightarrow AE\perp BC\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AE\perp\left(BCC'B'\right)\)
\(\Rightarrow AE=d\left(A;\left(BCC'B'\right)\right)\)
Ta có: \(AE=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(\Rightarrow d\left(A;\left(BCC'B'\right)\right)=\dfrac{a\sqrt{3}}{2}\)
\(MN//A'B\) (đường trung bình) \(\Rightarrow MN//D'C\)
Trong mặt phẳng \(\left(CDD'C'\right)\) từ P kẻ \(PQ//D'C\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow PQ\) là đường trung bình tam giác\(C'CD'\Rightarrow Q\) là trung điểm \(C'D'\)
Trong mặt phẳng \(\left(ABB'A'\right)\) kéo dài MN cắt \(A'B'\) tại F
\(\Rightarrow A'F=AM=\frac{1}{2}AB=\frac{1}{2}C'D'=D'Q\)
Trong mặt phẳng \(\left(A'B'C'D'\right)\) nối Q và F cắt \(A'D'\) tại E
Theo định lý Talet: \(\frac{A'E}{ED'}=\frac{A'F}{D'Q}=1\Rightarrow E\) là trung điểm \(A'D'\)
Tương tự MN kéo dài cắt \(BB'\) tại I, nối P và I cắt BC tại G
\(\Rightarrow G\) là trung điểm BC
Thiết diện cần tìm là lục giác MNEQPG
Nó chẳng là hình gì cả, khi hình hộp là lập phương thì đây là lục giác đều