Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

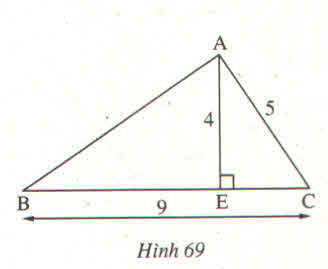
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)

a) Áp dụng định lí Pytago vào ΔAEC vuông tại E, ta được:
\(AC^2=AE^2+EC^2\)
\(\Leftrightarrow EC^2=AC^2-AE^2=5^2-4^2=9\)
hay EC=3(cm)
Vậy: EC=3cm
Ta có: BE+EC=BC(E nằm giữa B và C)
nên BE=BC-EC=9-3=6(cm)
Vậy: BE=6cm
Áp dụng định lí Pytago vào ΔABE vuông tại E, ta được:
\(AB^2=AE^2+BE^2\)
\(\Leftrightarrow AB^2=6^2+4^2=52\)
hay \(AB=2\sqrt{13}cm\)
Vậy: \(AB=2\sqrt{13}cm\)
b) Chu vi của tam giác ABC là:
\(AB+AC+BC=2\sqrt{13}+5+9=14+2\sqrt{13}cm\)


a) Ta có DE // AB, DF // AC, EF // BC. Vì EF // BC và DE // AB, theo định lí Thales, ta có:AB/BC = DE/EF. (1)Vì EF // BC và DF // AC, theo định lí Thales, ta có:AC/BC = DF/EF. (2)Từ (1) và (2), ta có:AB/BC = DE/EF = AC/BCRút gọn phương trình, ta được:AB = AC = BCVậy tam giác ABC = tam giác CEA.b) Vì AB = AC và DE // AB, theo định lí Thales, ta có:AB/DE = AC/CEVì vậy, AB = AC phải bao hàm DE = CE.c) Vì AB = BC và DE // AB, theo định lí Thales, ta có:AB/DE = BC/AEVì vậy, AB = BC phải suy ra DE = AE.d) Để chứng minh trung điểm 2 đoạn AC và BE trùng nhau, ta cần chứng minh rằng AE = EC và BD = DC.Vì DE // AB và DE = AE, theo định lí Thales, ta có:AB/DE = BC/ECVì thế,

a: Xét ΔAEB và ΔAEC có
AE chung
góc BAE=góc CAE
AB=AC
=>ΔAEB=ΔAEC
b: EB=6/2=3cm
=>AE=4cm

a: AC=5cm
b: Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
\(\widehat{CAE}=\widehat{KAE}\)
Do đó: ΔACE=ΔAKE
Suy ra: AC=AK; EC=EK
=>AE là đường trung trực của CK
hay AE⊥CK
c: Xét ΔEAB có \(\widehat{EAB}=\widehat{EBA}\)
nên ΔEAB cân tại E
mà EK là đường cao
nên K là trung điểm của AB
hay KA=KB
Áp dụng định lý pitago vào tam giác vuông AEC ta có:
AC2=AE2+EC2
=>EC2=AC2-AE2=52-42=25-16=9
=>EC=3M
Ta có: BC = BE + EC
BE = BC – EC = 9 – 3 = 6(m)
Áp dụng định lí pitago vào tam giác vuông AEB, ta có:
AB2=AE2+EB2=42+62=16+36=52
Suy ra: AB = √52(m) ≈7,2m