Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi là một điểm của đoạn thẳng ta có:
Mà
Diện tích hình chữ nhật là:
Diện tích hình tam giác là:
Diện tích tam giác bằng
Chúc học tốt!

Ta có: \(S_{AMN}=\frac{BN.AM}{2}=\frac{BN\cdot\frac{1}{2}AB}{2}\)
\(S_{ABN}=\frac{AB.BN}{2}\)
=> \(\frac{S_{AMN}}{S_{ABN}}=\frac{\frac{\frac{1}{2}BN.AB}{2}}{\frac{AB.BN}{2}}=\frac{1}{2}\) => \(S_{AMN}=\frac{1}{2}S_{ABN}\)(1)
Ta lại có: BN = 2NC; BN + NC = BC => BN = 2/3BC
\(S_{ABN}=\frac{AB.BN}{2}=\frac{AB\cdot\frac{2}{3}BC}{2}\)
\(S_{ABCD}=AB.BC\)
\(\frac{S_{ABN}}{S_{ABCD}}=\frac{\frac{\frac{2}{3}AB.BC}{2}}{AB.BC}=\frac{1}{3}\) => \(S_{ABN}=\frac{1}{3}S_{ABCD}\) => \(\frac{1}{2}S_{ABN}=\frac{1}{6}S_{ABCD}\)(2)
Từ (1) và (2) => \(S_{AMN}=\frac{1}{6}S_{ABCD}\)
awbb ưieaaaaaaaa
r
ewfrsd
tf
sdfdyufee
e
ẻ
r
re
ê
r
e
ẻ
e
re
ẻ
rr

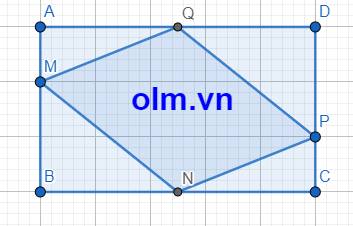
SAMQ = \(\dfrac{1}{2}\)AM\(\times\)AQ = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{1}{3}\)AB\(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{12}\)SABCD
BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB
SBMN = \(\dfrac{1}{2}\)BM\(\times\)BN = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{2}{3}\)AB\(\times\)\(\dfrac{1}{2}\)BC = \(\dfrac{1}{6}\)SABCD
SCPN = \(\dfrac{1}{2}\)CN \(\times\) CP = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{1}{2}\)BC\(\times\)\(\dfrac{1}{3}\)CD = \(\dfrac{1}{12}\)SABCD
DP = CD - CP = CD - \(\dfrac{1}{3}\)CD = \(\dfrac{2}{3}\)CD
SDPQ = \(\dfrac{1}{2}\)DP\(\times\)DQ = \(\dfrac{1}{2}\)\(\times\)\(\dfrac{2}{3}\)CD \(\times\)\(\dfrac{1}{2}\)AD = \(\dfrac{1}{6}\)SABCD
SMNPQ = SABCD - (SAMQ + SBMN + SCPN + SDPQ)
Phân số chỉ diện tích của tứ giác MNPQ là:
1 - \(\dfrac{1}{12}\) - \(\dfrac{1}{6}-\dfrac{1}{12}-\dfrac{1}{6}\) = \(\dfrac{1}{2}\) (SACBD)
Diện tích của tứ giác MNPQ là:
360 \(\times\) \(\dfrac{1}{2}\) = 180(cm2)
Đáp số: 180 cm2

SQAM = SQDP = \(\dfrac{1}{6}\) SABCD = 48 cm2
SMBN = SPNC = \(\dfrac{1}{12}\) SABCD = 24 cm2
Diện tích hình MNPQ là:
288 - (48 + 24) x 2 = 144 (cm2)
Đáp số: 144 cm2
Kẻ 2 đường chéo của MNPQ lần lượt là MP; NQ
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì AM =2/3 AB => MB = 1/3AB
=> Vì AB = DC => 1/3 AB = 1/3CD => MB = CP
=> Kẻ đường chéo thứ nhất từ M xuống C = Chiều rộng của hcn ABCD
Vì BN = NC ; DQ = QA
=> Vì BC =AD=> BN = NC = DQ = QA
=> Kẻ đường chéo thứ 2 từ N sang Q = Chiều dài của hcn ABCD
=> SMNPQ = NQ*MP : 2
Mà NQ = AB và MP = BC
=> SMNPQ = AB* BC : 2
Mà AB*BC= 288
=> SMNPQ = 288 : 2
SMNPQ = 144 (cm2)

\(S_{BMN}=\dfrac{1}{2}xBMxBN=\dfrac{1}{2}x\dfrac{AB}{4}x\dfrac{BC}{2}=\dfrac{1}{16}xS_{ABCD}\)
\(S_{CPN}=\dfrac{1}{2}xCNxCP=\dfrac{1}{2}x\dfrac{BC}{2}x\dfrac{CD}{2}=\dfrac{1}{8}xS_{ABCD}\)
\(S_{DPQ}=\dfrac{1}{2}xPDxDQ=\dfrac{1}{2}x\dfrac{CD}{2}x\dfrac{AD}{3}=\dfrac{1}{12}xS_{ABCD}\)
\(S_{AMQ}=\dfrac{1}{2}xAMxAQ=\dfrac{1}{2}x\dfrac{3xAB}{4}x\dfrac{2xAD}{3}=\dfrac{1}{4}xS_{ABCD}\)
\(\Rightarrow S_{MNPQ}=S_{ABCD}-\left(S_{BMN}+S_{CPN}+S_{DPQ}+S_{AMQ}\right)\)
Bạn tự thay số rồi tính nốt nhé

HD:
Tính diện tích các tam giác vuông: AMQ; MBN; NCP và PDQ
Lấy diện tích hình chữ nhật ABCD trừ đi tổng diện tích 4 tam giác vuông trên sẽ được diện tích hình tứ giác MNPQ
\(S_{AMD}=\dfrac{1}{2}\cdot AM\cdot AD=\dfrac{1}{4}\cdot S_{ABCD}\)
\(S_{MBN}=\dfrac{1}{2}\cdot BM\cdot BN=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot AB\cdot\dfrac{1}{4}\cdot BC=\dfrac{1}{16}\cdot S_{ABCD}\)
\(S_{NCD}=\dfrac{1}{2}\cdot DC\cdot CN=\dfrac{1}{2}\cdot\dfrac{3}{4}\cdot DC\cdot BC=\dfrac{3}{8}\cdot S_{ABCD}\)
=>S MND=5/16*S ABCD
=>S ABCD=14:5/16=44,8cm2